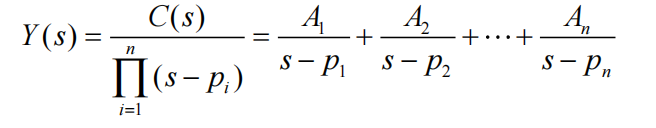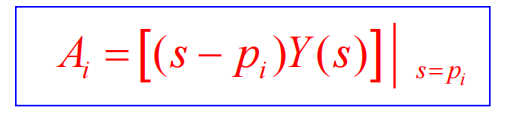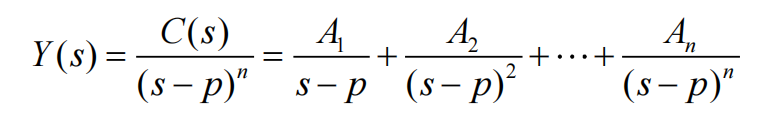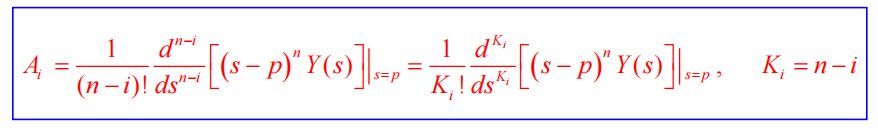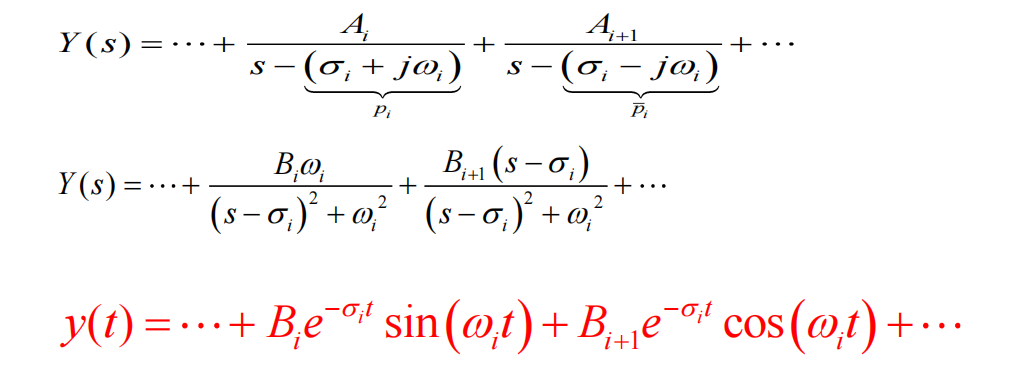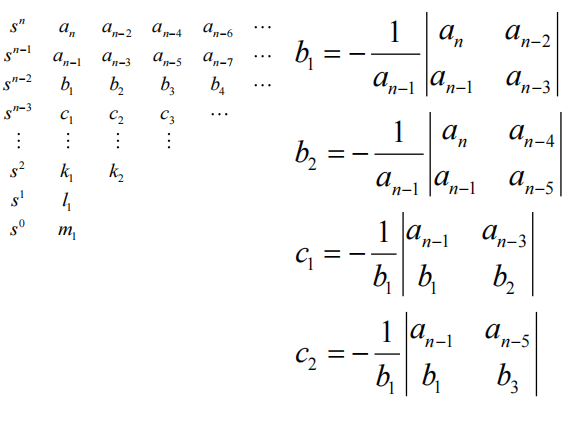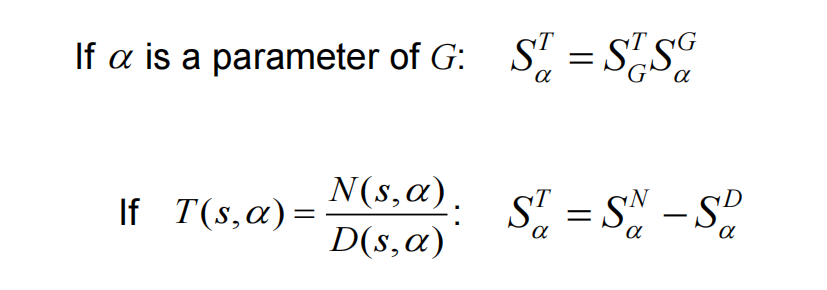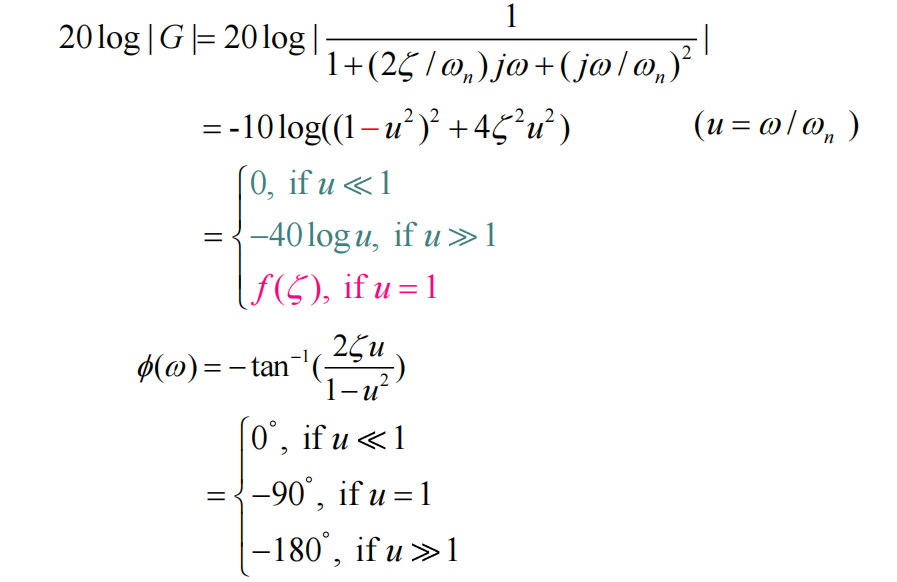Matlab & Math & Simulink
Matlab
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
|
p=[1 2 3 4];
r=roots(p);
p=poly(r);
p=[1 2];q=[3 4];
r=conv(p,q);
value=polyval(r,1);
a=[1 2];
b=[3 4];
sys=tf(a,b);
pole(sys);zero(sys);
[P,Z]=pzmap(sys);
sys=series(sys1,sys2);
sys=parallel(sys1,sys2);
sys=feedback(sys1,sys2,sign);
sys=minreal(sys1);
t=[0:0.001:5];
[y,t]=step(sys,t);plot(t,y)
p(;,2)
syms t s a
F1=laplace(sin(a*t),t,s);
F2=ilaplace(F1,s,t);
lsim(num,den,u,t)
lsim(sys,u,t)
sys=zpk(z,p,1);
[R,K]=rlocus(sys);
rlocus(num,den)
[K,poles]=rlocfind(num,den)
bode(sys)
Nyquist(sys)
|
Simulink
simulink 无法向前兼容,但是可以保存为之前的版本文件
常用模型
- gain:K
- integrator: s1
- transfer FCN:一般s分式表达
- Scope:示波器
- Step:阶跃信号
Math
部分分式法求逆Laplace
-
单实根
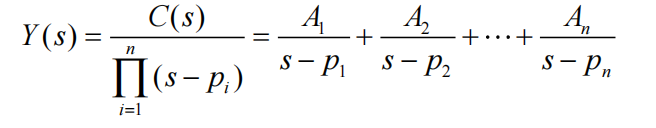
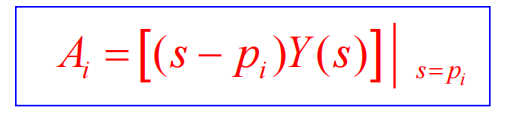
-
重实根
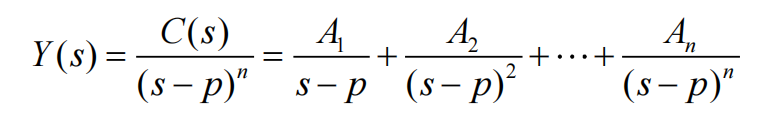
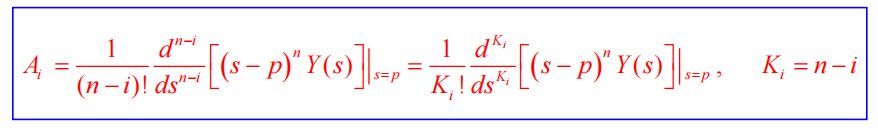
乘(s−p)i,求n−i阶导,除(n−i)!
-
复数根
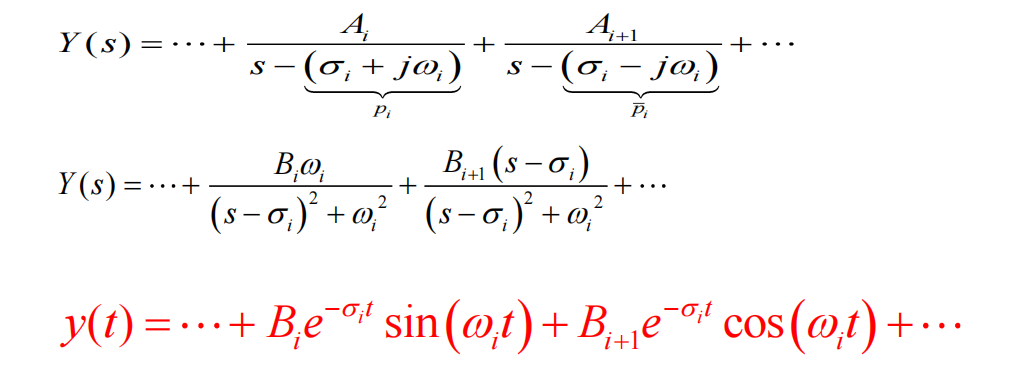
原式纯实系数:Ai&Ai+1必然共轭,可以通过case1求解
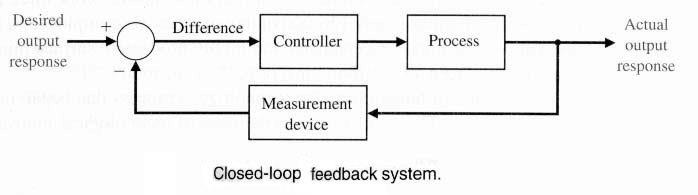
Basic Concepts
-
Controller: brain
-
Sensor: eye
-
Actuator: hand
-
Process: 有时候将Actuator包含在内
-
Controlled Variables / Output Variables: quantify the performance of the final product
-
Manipulated Variables / Input Variables: adjusted dynamically to keep the controlled variables at their set-points
“被操纵变量”是指为了控制或控制输出而要操作的变量。
如空调的电流,或炉子的燃料
-
Disturbance Variables / Load Variables: cannot be adjusted and may deviate controlled variables
-
Set-point change: servo control
-
Disturbance / Load change: regulatory control
-
Feedback: 一种有评估性信息的结果返回
Equivalent Block Diagram
- 引出点:引出点是没有顺序的,可以理解成在一条干路上引出两个支路,其代表的数值都是相同的
- 比较点:比较点是表示那两个信号在此处相加或者相减
-
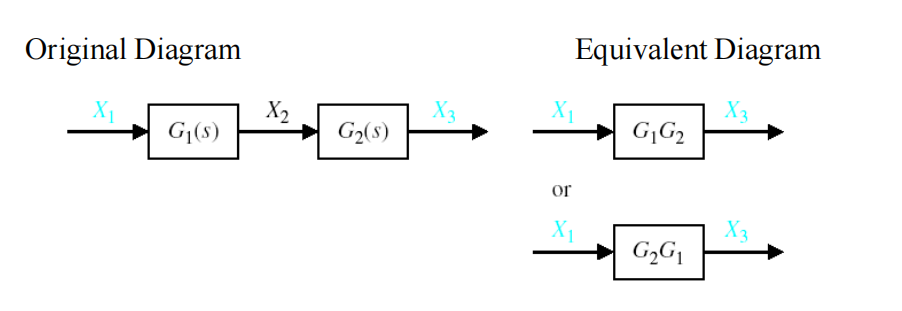
串联等效
(X1G1)G2=X1(G1G2)=X1(G2G1)
-
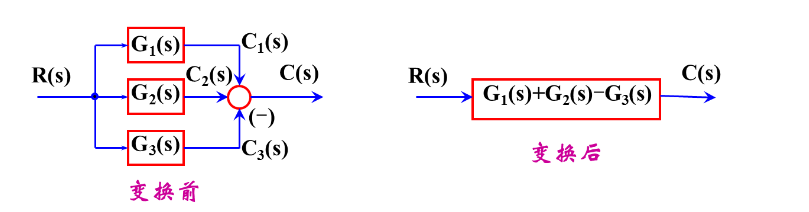
并联等效
RG1+RG2+RG3=R(G1+G2+G3)
-
反馈等效
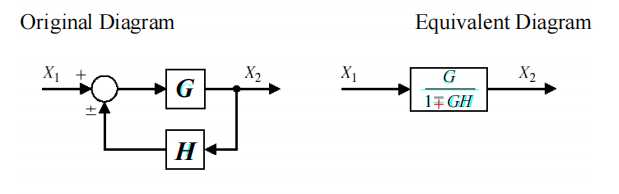
-
比较点前移
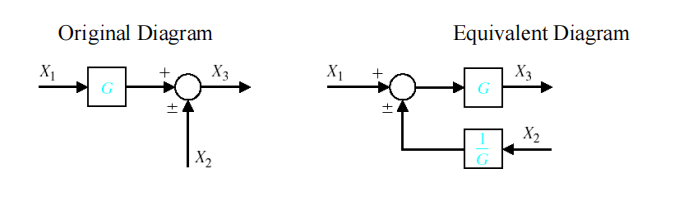
-
比较点后移
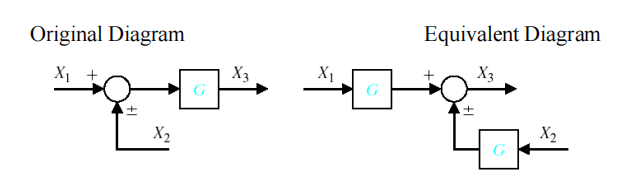
-
引出点前移
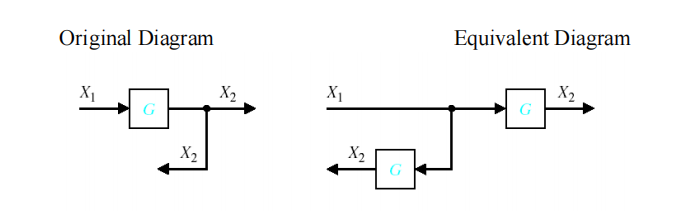
-
引出点后移
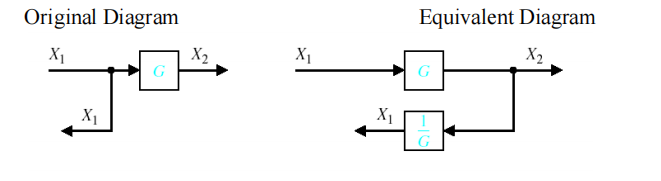
-
相邻比较点交换&合并
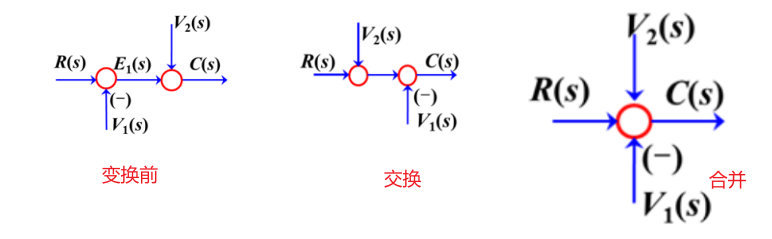
(显然的!)相邻引出点也可以交换位置,但引出点比较点相邻,不可互换位置
应用框图的等效变换计算: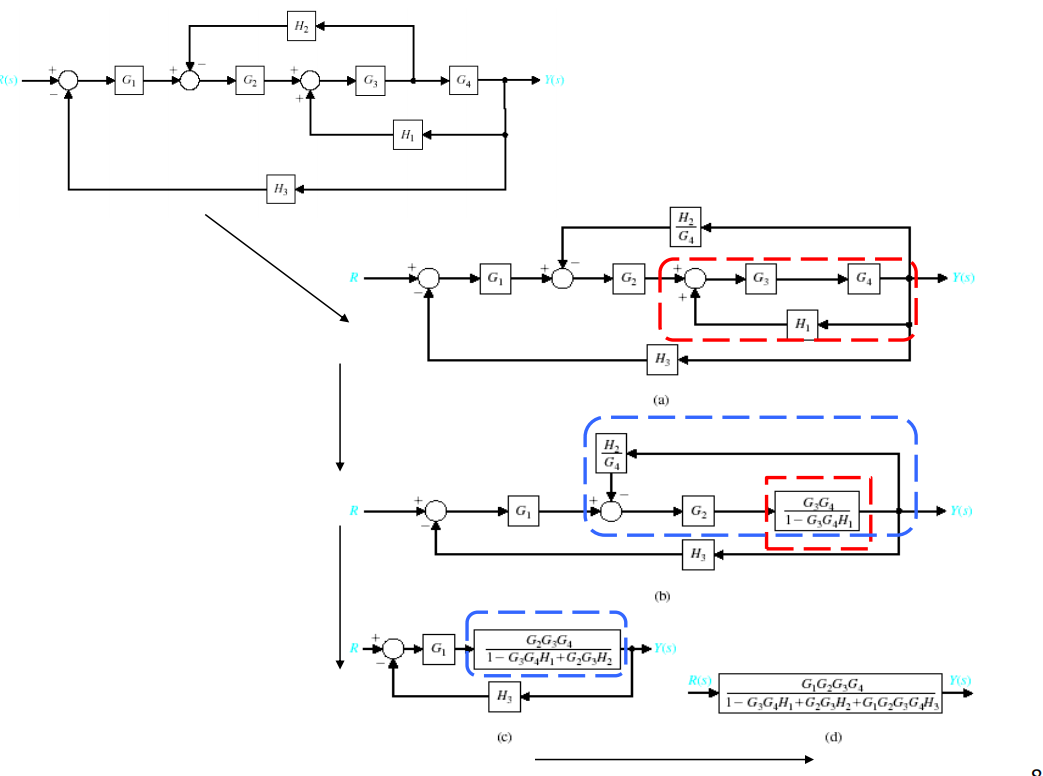
Signal Flow Graph(SFG)
信号流图:框图的简化

- 混合点:SFG中同时实现了比较和引出的节点
- Forward Path前向支路: 从输入到输出,并与每个节点相交至多一次
- Non-touching Loops: two loops with no common node(一个点也不行)
-
SFG绘制时候不能忽略输入输出的这两条:
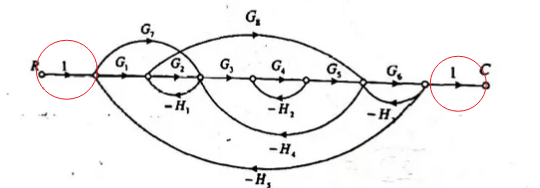
-
将block diagram转为SFG时需要小心节点的画法: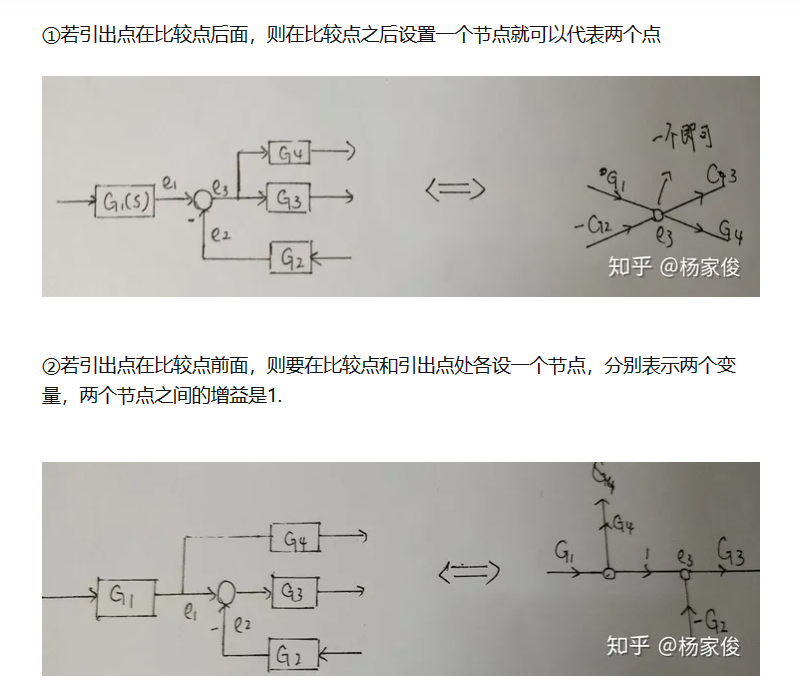
Mason’s Rule
适用Block Diagram & Signal Flow Graph,直接计算传递函数
Δ配合Routh Array判定稳定性

-
注意计算回路增益Li时的正负号
-
梅森公式用于输入和输出节点,即不能在混合节点使用: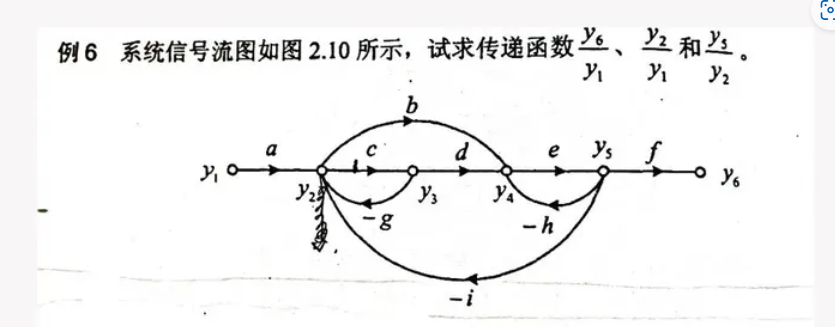
计算y5/y2时:y5是引出点,y2是混合节点,Mason要求两都不是混合节点
所以需要计算y2/y1和y5/y1传递函数再相除得y5/y2传递函数
-
没有接触的回路指完全没有接触,一个点也不行
-
前向支路中节点也不能重走
General Responses
传递函数表示法只适用于LTI系统
非LTI(MIMO)系统需要State Space状态空间表示法
S域
时域
Transfer Functions
各个闭环传递函数的值可以通过对应置零后,重画框图,套用反馈公式得到
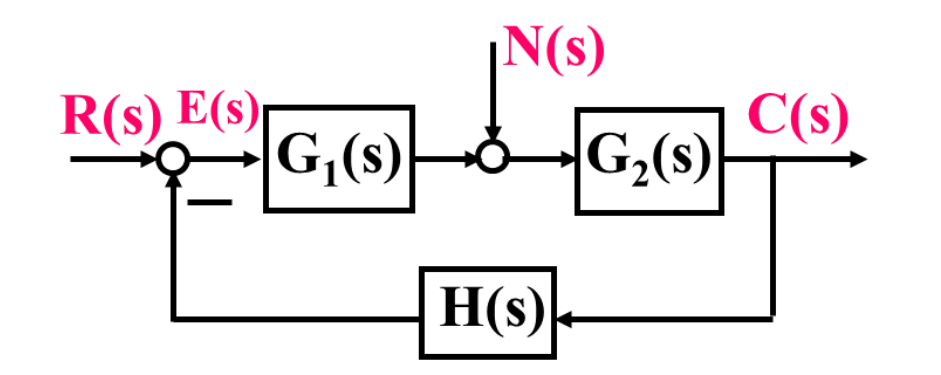
系统开环传递函数(Loop Gain)
G1(s)G2(s)⋅H(s)
表示反馈信号和误差信号E(s)的比值
系统闭环传递函数
- C(s)对R(s):N(s)=0→ϕ(s)=C(s)/R(s)=1+G1(s)G2(s)H(s)G1(s)G2(s)
- C(s)对N(s):R(s)=0→ϕn(s)=C(s)/N(s)=1+G1(s)G2(s)H(s)G2(s)
- 叠加原理:C(s)=ϕ(s)R(s)+ϕn(s)N(s)
系统闭环误差传递函数
- E(s)对R(s):N(s)=0→ϕe(s)=E(s)/R(s)=1+G1(s)G2(s)H(s)1
- E(s)对N(s):R(s)=0→ϕen(s)=E(s)/N(s)=1+G1(s)G2(s)H(s)−G2(s)H(s)
- 叠加原理:E(s)=ϕe(s)R(s)+ϕen(s)N(s)
Step Response
Why Step response
-
可以体现系统全部响应特征,之后使用叠加、求导等可以得到其余基础响应
例如:δ(t)=u˙(t)→y1(t)=y˙(t)
-
input: u(t)
-
s plane: s1
1st order system
τy˙+y=Ku
-
τ:time constant
-
K:dc gain
-
T(s)=τs+1K,pole=−1/τ<0(if stable),no zeros
-
y(t)=K(1−e−t/τ)
The smaller τ is,
the steeper the initial slope is,
the faster the response approaches the steady state.
2nd order system
y¨+a1y˙+a0y=b1u˙+b0u
- T(s)=s2+a1s+a0b1s+b0,p1,2=2−a1±a12−4a0,z=−b0/b1
- if stable:a1>0,a0>0
standard form of stable 2nd order system without zeros
y¨+a1y˙+a0y=b0u⇒y¨+2ξwny˙+wn2y=Kwn2u
-
ξ:damping ratio
-
wn:natural frequence
-
K:dc gain
-
p1,2=−ξwn±ξ2−1wn=−σ±wd
-
wd:damped angular (or circular) frequency
-
ξ>1:over damped
→y(t)=c1e−r1t+c2e−r2t
-
ξ=1:critically damped
→y(t)=e−rt(c1t+c2)
-
0<ξ<1:under damped
→y(t)=K[1−1−ξ21e−σtsin(wdt+θ)],θ=cos−1ξ
under damped characteristics
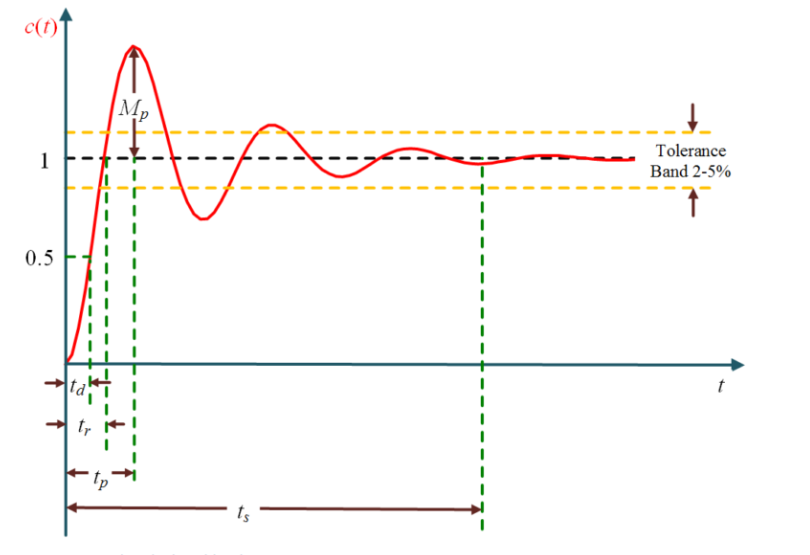
-
delay time (0→50%) td=wn0.7ξ+1
-
peak time tp=wdnπ
-
rise time (10%→90%) tr=wdπ−θ
-
Overshoot Mp=ymax−yss=Ke−ξπ/1−ξ2
-
percent overshoot %MP=yss−y0Mp×100%=e−π/tanθ×100%
-
x% band settling time ts:differ between tolerance bands
| % |
1% |
2% |
5% |
| ts(τ=1/σ) |
4.6τ |
3.9τ |
3.0τ |
for a nondominant third pole
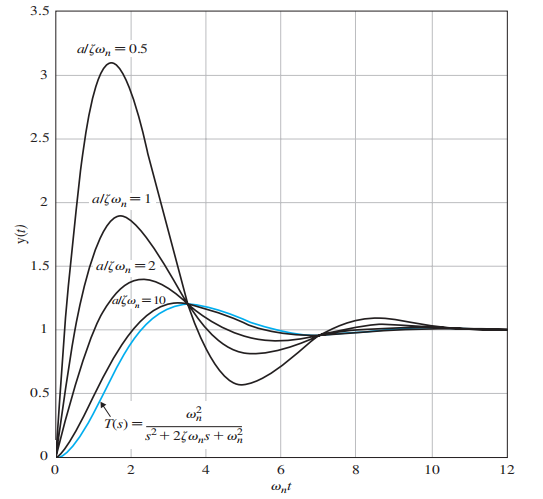
T(s)=(s2=2ξs+1)(γs+1)1
∣1/γ∣≥10∣ξwn∣: 近似忽略主极点实部十倍外极点,反之不可忽略
for a zero
T(s)=s2+2ξwns+wn2awn2(s+a)
Routh-Array for Stability
A linear time invariant (LTI) system is stable if and only if (iff) its free response converges to zero for all ICs.
BIBO:有界输入⇒有界输出
通用的判定LTI系统稳定性方式:Routh-Hurwitz Criterion(充分必要的!!)
给出了判别实系数多项式有无实部非负根(非LHP平面极点)的充要条件
-
建立Routh Array(补0)
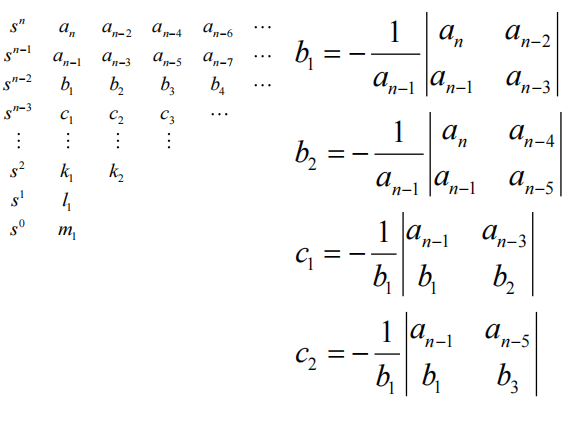
-
多项式所有零点都位于左半平面等价于「Routh Array首列元素都为正」(如果不是,那么符号改变的次数即为右半平面根的个数
正负正,符号改变了两次
-
零的特殊情况
-
当某行有0元素出现时,而且这个0后面还有非零元素时。
此时计算劳斯判据时将0替换成epsilon,然后继续算其它未知元素,最后令epsilon趋向于0+,得到的第一列元素若发生符号的改变,那么系统是不稳定的
-
当某一行整行都是0的时候
此时把全0行的上一行列出P(s)表达式,对P(S)进行求导后把得到的系数填到原本是全零行的地方
Case1大概率不稳定,Case2必然不稳定(若认为临界稳定也不稳定)
Case2 occurs when there is an even polynomial factor(因式) such as s2+a,s4+b,s4+as2+b
即全零行上一行的式子为p(x)的因子式
-
可用Mason’s law得到Δ即q(s)后使用Routh-Hurwitz Criterion判定稳定性
Feedback
System Error
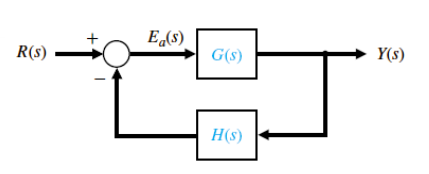
Y(s)=1+GHGR(s): system error E(s)=R(s)−Y(s); Ea(s)=R(s)−HY(s)
Closed Loop System: E(s)=1+GH1+GH−GR(s),Ea(s)=1+GH1R(s)
Sensitivity
G(s)&H(s) may vary due to the environment and exits ΔG&ΔH:
Closed loop System:ΔY≈(1+GH)2ΔGR<<ΔGR(open loop system)
Define: Sab=sensitivity from a to b=∂a/a∂b/b (越小越好)
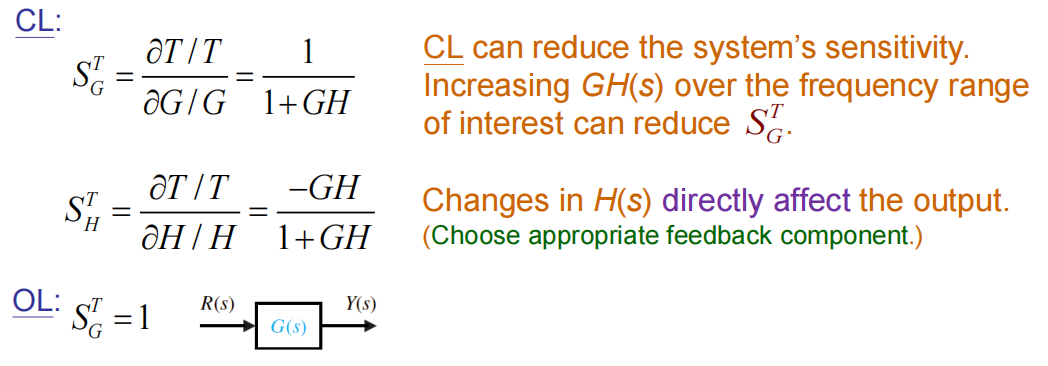
反馈器H(s)往往要求做的精确且稳定!!
运算法则:
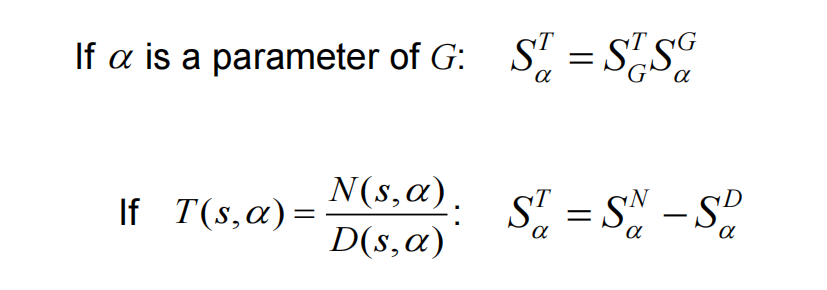
Influence
-
影响稳定性:可能引发系统不稳定
-
影响瞬态响应速度:本质影响 τ
-
影响Sensitivity:用增益换线性度
-
影响DC值&Steady State Error
-
影响抗干扰能力:本质影响干扰的传输函数&输出对干扰的Sensitivity
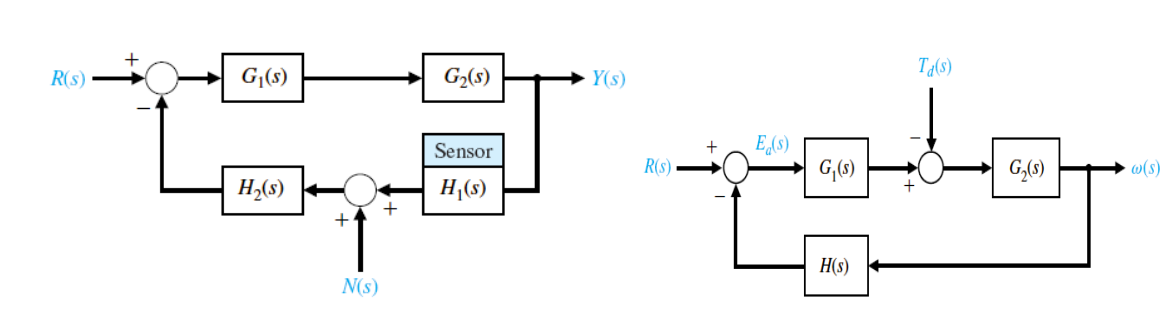
- 第一种Disturbance:Y(s)≈−H11N(s),SH1T≈1
- 第二种Disturbance:Y(s)≈−G1H1Td(s),SH1T≈1
反馈器H(s)需要大且稳定!!
Standard Test Signals
r(t)=tn & R(s)=sn+1n!
Under-damped 2nd system 常用参数
- %MP=5%→ξ>0.69 & θ<46°
- θ=cos−1ξ=tan−1(1−ξ2/ξ)=tan−1(1−ξ2wn/ξwn)表示夹角
估算ξ
Method1
- tp=βwnnπ,N( cycle numbers in 1s )=2nπ/βwn1
- cycles are visible in 4τ s:2% settling time
- Numbers of cycles visibe:4τ⋅2nπ/βwn1=2πξ4β=πξ21−ξ2
Method2
- percent overshoot %MP=yss−y0Mp×100%=e−π/tanθ×100%=e−πξ/1−ξ2×100%
定性分析
- 稳定性:极点都在LHP平面
- 快速性:极点远离虚轴
- 平滑性:θ越小,越平滑(极限都是实极点无超调)
Steady State Error
Unit Feedback H(s)=1
Standard input signals r(t)=tn & R(s)=sn+1n!
G(s)=sN∏(s+pk)K∏(s+zi), Loop Gain=G(s)⋅H(s)=G(s)
E(s)=R(s)−Y(s)=1+G(s)1R(s),ess=lims→0sE(s)
N:System Type Number 原点处极点个数
|
ess |
| N<n |
∞ |
| N=n |
1+K∏zi/∏pkA |
| N>n |
0 |
常用三阶及以下系统ess的有限值计算

- Kp=lims→0G(s)
- Kv=lims→0sG(s)
- Ka=lims→0s2G(s)
Nonunity Feedback H(s)=1
-
Equivalent Block Transformation
等效变换系统框图使得H(s)=1
-
直接计算
- ISE=∫0Te2(t)dt
- IAE=∫0T∣e(t)∣dt
- ITSE=∫0Tte2(t)dt
- ITAE=∫0Tt∣e(t)∣dt
T:usually equals Ts
General form of the performance integral is I=∫f(e(t), r(t), y(t), t) dt
Optimal Control: Adjust system parameters to min/max the performance index
Standard input signals的系统指标对应最优化系数:可以查表
System Simplification
To approximate a high-order system using a lower-order system, with a minimum difference in the system property of interest.

利用M2q=Δ2q(q=1,...)求解ci,di
有时用低阶系统近似高阶系统需要保留其主极点
将L(s)的分母用主极点表示 ∏(s+pi)
分子相应变化即可(M2q=Δ2q(q=1,...))
Root Locus
开环增益G(s)=P(s)Z(s),反馈H(s): Loop Gain L(s)=G(s)H(s)
→闭环传递函数T(s)=1+GHG=P(s)+HZ(s)Z(s),特征根方程L(s)=−1
→1+HP(s)Z(s)=0, P(s)+HZ(s)=0
当一个parameter K从0变化到 ∞时,闭环特征根的轨迹变化,进而判定相关特性
以反馈H为例:H从0→∞时,特征根从P(s)=0→Z(s)=0,即从极点变化到零点
如何快速绘制根轨迹图?
化为 standard form & 应用 rules进行特定 Procedures
调整Δ(s)的表达式,使之形成:1+kP(s)Z(s)=0形式
分子m阶,分母n阶,K是从0→∞的参数
幅角条件
- k⋅∣P(s)∣∣Z(s)∣=1
- ∠Z(s)−∠P(s)=(2t+1)π,t∈Z
广义根轨迹
- 参数根轨迹:进行等式变换,得到以参数为根轨迹增益的等效传递函数
- 0°根轨迹:对应正反馈形式,即kP(s)Z(s)=1
8 Rules
-
起点&终点:开环极点指向开环零点/无穷远处
-
n条分支:开环极点数(系统阶数)
-
对称性:根轨迹关于实轴对称
-
分离点(对应重根):dsdP(s)Z(s)=0 OR ∑d−pi1=∑d−si1
-
虚轴交点:s=jw代入特征根方程反解 OR 采用Routh Array 求解
-
实轴上根轨迹存在性
- 180°根轨迹:右侧极点数目+零点数目=奇数,存在根轨迹
- 0°根轨迹:右侧极点数目+零点数目=偶数,存在根轨迹
-
渐近线:实轴交点在n−m∑pi−∑zi
- 180°根轨迹:φ=n−m(2t+1)π
- 0°根轨迹:φ=n−m(2t)π
-
出射角&入射角
- 180°根轨迹:θout=(2t+1)π+∑∠zp−∑∠pp
- 180°根轨迹:θin=(2t+1)π+∑∠pz−∑∠zz
- 0°根轨迹:θout=2tπ+∑∠zp−∑∠pp
- 0°根轨迹:θin=2tπ+∑∠pz−∑∠zz
零点为入射角,指向零点;极点为出射角,指向极点
Tips:同型相减,异型相加
当存在重合的零点或极点:aθ,a:该点重合的零点或极点个数
180°根轨迹:奇数,(2t+1)π
0°根轨迹:偶数,2tπ
Proof (以180°根轨迹为例)

Hints
-
n−m≥2: 根的和为定值
P(s)+kZ(s)=0,韦达定理中K无法影响 sn−1系数
-
若系统有2个开环极点,1个开环零点,且在复平面存在根轨迹, 则复平面的根轨迹一定是以该零点为圆心的圆弧
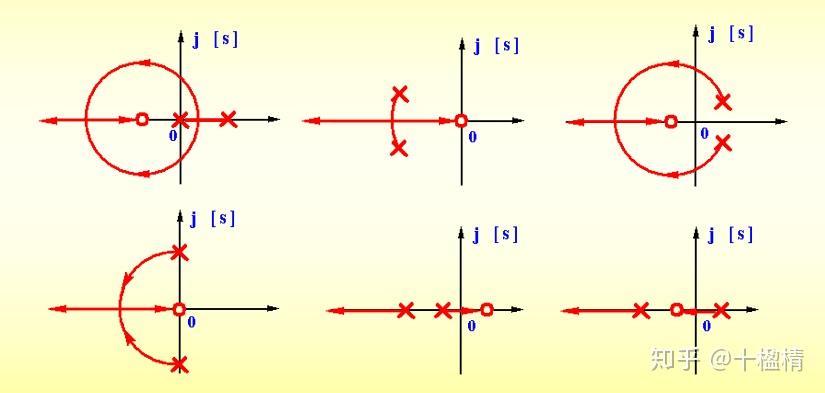
Proof:s=σ+jw代入或利用实系数共轭 s=σ±jw配合韦达定理消k
实际上,当存在2个极点&1~2个零点&根轨迹复平面存在,均为圆弧
自动控制原理“轨迹圆”若干问题的探讨 - 更多讨论
-
开环零点对根轨迹影响:吸引渐近线,可以使得不稳定系统转向稳定
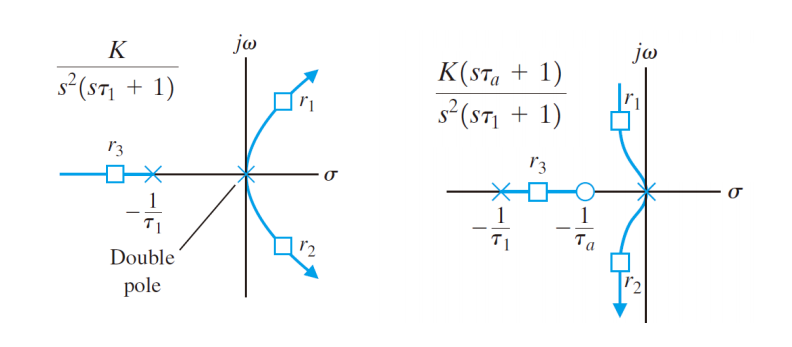
Procedures
- 转化为Standard form
- s-plane图中标出零极点
- 确定实轴存在根轨迹区域
- 计算渐近线(与实轴交点、角度)
- 计算分离点
- 计算虚轴交点
- 计算各个零极点的入/出射角
Frequency Response
Basic Concepts
Bode Plots
Precise Calculation
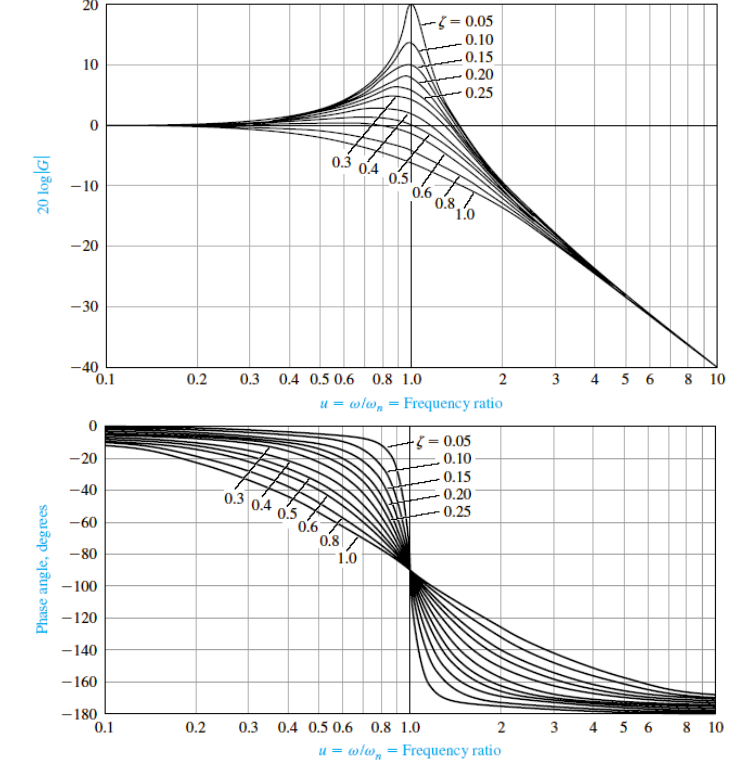
Bode Plot是指系统开环增益L(s)=G(s)H(s)的相频曲线和幅频曲线,若得到了L(s)的表达式,即零极点位置和开环静态增益可以精确绘制
Pole-Zero Diagram可以形象描绘并观测频率响应特性
以一对复数极点为例分析:
G(jw)=1+(2ξ/wn)jw+(jw/wn)21
- 20log∣G∣=−20log(1−w2/wn2)2+4ξ2w2/wn2
- ϕ=−tan−1(wn22ξwn−w2)
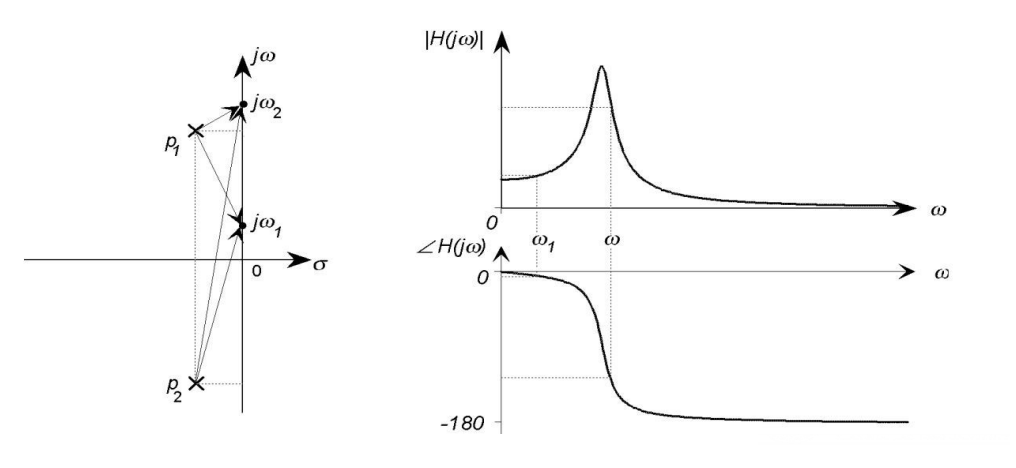
在Pole-Zero Diagram中可以看出,magnitude和jw到两个极点p1,2的长度乘积有关,可能存在极值(称谐振频率wr),对应幅频曲线极值(称谐振峰值Mp)
Bode Plot的精确图&极值具体表达式和ξ的大小相关:
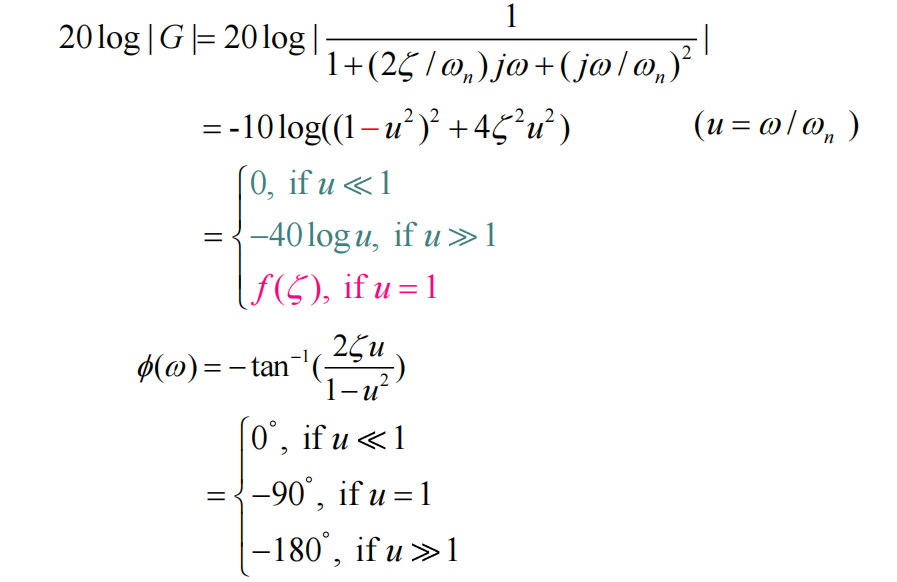
-
0<ξ<21
幅频曲线存在极值,wr=wn1−2ξ2取到最大值2ξ1−ξ21
-
21≤ξ<1
幅频曲线单调递减,不存在极值;ξ=21时恰好wr=wn
-
ξ=0
wn=0→Mp=∞,即无阻尼系统输入信号频率恰好为wn时会输出无穷大幅度的信号,即发生了共振!(可用荡秋千想象)
其他情况(较为简单,直接计算幅度&相位即可)

Quick Estimation
在电路设计时候需要快速画出Bode Plot的近似图表
Bode定理
利用最小相位系统、远离的零极点的幅度(绝对值)快速绘制Bode Plot
此时零极点:实际零极点的模
对频率响应的影响和实际零极点所处平面有关、可以叠加
| 零极点 |
增益变化 |
零极点处 |
十倍频率外 |
备注 |
| 左极点 |
-20db/dec |
-3dB&-45° |
-90° |
减低gain&phase |
| 右极点 |
-20db/dec |
-3dB&+45° |
+90° |
系统必然不稳定 |
| 左零点 |
+20db/dec |
+3dB&+45° |
+90° |
提升gain&phase |
| 右零点 |
+20db/dec |
+3dB&-45° |
-90° |
提升gain、降低phase |
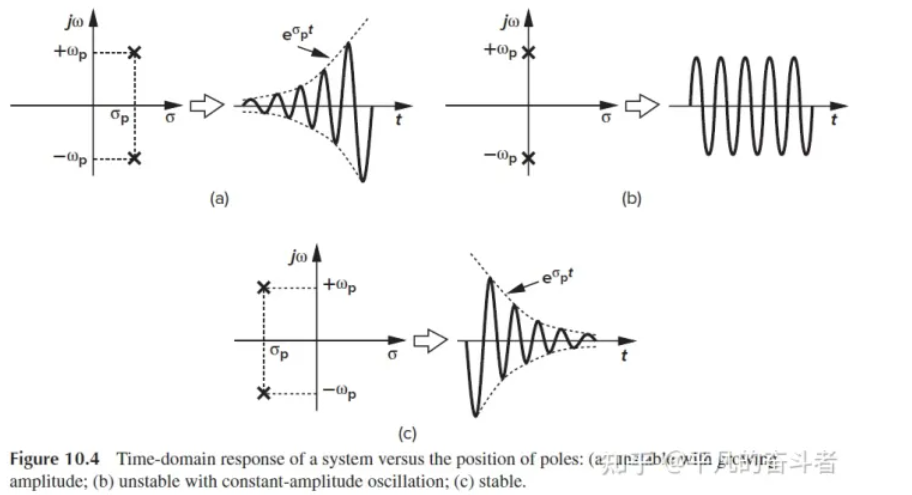
极点不同位置对系统稳定性影响(不稳定、等幅震荡、阻尼震荡稳定)
- 零点都是增大gain,极点都是减小gain
- 对phase影响需要看平面
以上节的一对复数极点分析为例:当w靠近0和趋向无穷,幅度为0dB & -40dB/dec 相位为0 °&2*-90°,和Bode定理近似结果一致;只有在极点附近,近似忽略了幅度上wr处的Overshoot,而相位仍然-2*45°和和Bode定理近似结果一致
实际上,在模拟电路设计分析中,极点由RC形成,处于实轴上,不会出现一对复数极点的情况,则对单个零极点:Bode定理近似在幅度和相位上均一致!此时多个若能保持多个零极点远离,则能快速绘制Bode Plot
电路设计时,总是将零极点人为地远离
Nyquist Plot
本质是将精确的Bode Plot的幅频响应&相频响应绘制到一个极坐标中,描绘s=jw=0→∞时,G(jw)的变化趋势,又称 幅相特性曲线
Quick Estimation
- 利用Pole-Zero Diagram确定起点(s=j0)、终点(s=j∞)的幅度和相位
- 估算途中幅度和相位的变化趋势
- 如有必要,计算和实轴、虚轴的交点
- 绘制出Nyquist Plot草图
Common Cases
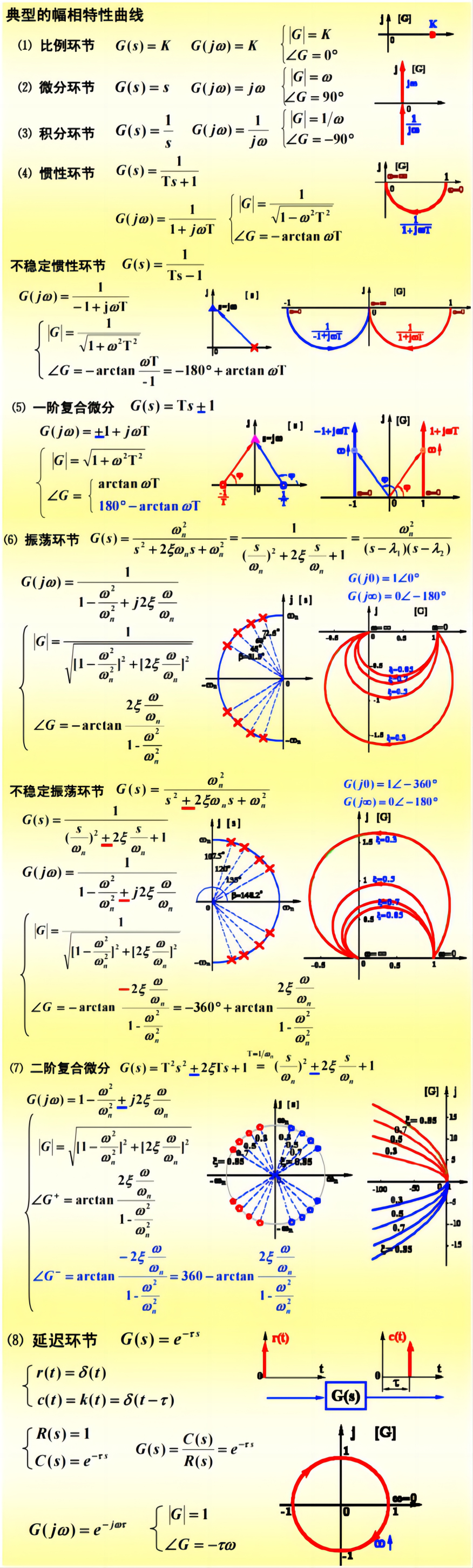
All in one: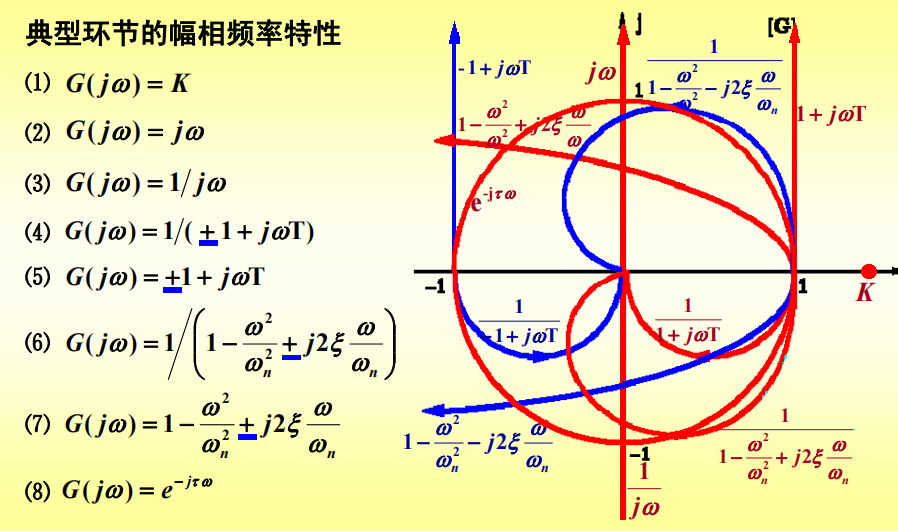
Stability
最准确的方式是采用Nyquist Criteria或Bode Criteria,但常常结合Barkhausen’s Criteria,直接用BodePlot上快速得出PM&GM来判断闭环系统的稳定性。这种方法是快速的但不是充分必要的(不准确的,在实际工程中存在一些特例会失效)
Nyquist
Math Foundations
映射定理
设复变函数F(s)=∏(s−pi)K∏(s−zi),s=σ+jw→F(s)=U+jV
设F(s)为解析函数(除s的有限奇点外)⇒对于s平面上不通过F(s)奇点的任一条闭曲线C1, 在F(s)平面上必有一条对应的映射曲线 T1
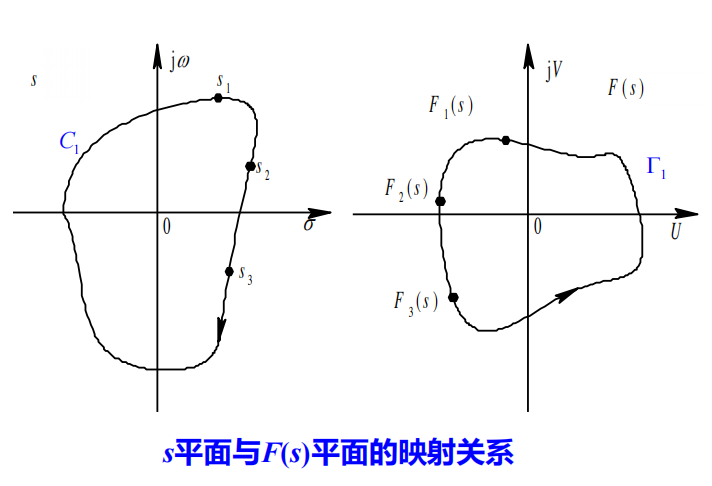
Cauchy辐角原理
s沿着闭曲线C1正向绕行一周后,F(s)辐角的改变量Δ∠F(s)=2π⋅(Z−P)
Z为C1内部零点F(s)个数,P为C1内部极点F(s)个数
应用到此处:设s平面上的封闭曲线包围了复变函数F(s)的P个极点和Z个零点,并且此曲线不经过F(s)的任一零点和极点,则当复变量s沿封闭曲线顺时针方向移动一周时,在F(s)平面上的映射曲按顺时针方向包围坐标原点Z-P周
Nyquist Criteria
开环传递函数G(s)H(s)=β∏(s−pi)∏(s−zi) ,闭环传递函数T(s)=1+G(s)H(s)G(s)
设F(s)=1+G(s)H(s)=1+β∏(s−pi)∏(s−zi)≜∏(s−pi)∏(s−λi)
⇒T(s)=∏(s−pi)G(s)∏(s−λi)
$\Rightarrow 闭环系统极点即F(s)的零点,判定稳定性即找到F(s)$的RHP零点数目即可
-
在s-plane上取奈氏回线,则奈氏回线包含F(s)的所有RHP零点&极点
奈氏回线:包围整个s-plane右侧平面的曲线,具体为一个按顺时针方向运动的封闭曲线,由整个虚轴和半径为∞的右半圆组成,圆心为原点
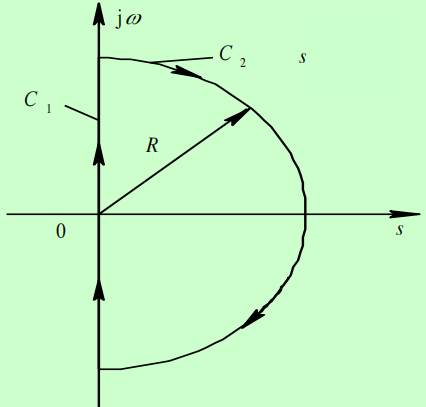
-
绘制出s-plane奈氏回线在F(s)平面上的映射曲线
-
当s沿虚轴由下而上运动,s=jw∣w=−∞→+∞,在F(s)平面轨迹类比NyquistPlot即可
-
当s在半径为∞的右半圆上运动,s=∞⋅eiθ∣θ=2π→−2π
F(s)=1+β∏(s−pi)∏(s−zi),s=reiθ∣θ=0→2π,取极限r→∞
分母阶数>分子阶数:F(s)=1+0=1
分母阶数=分子阶数:F(s)=1+β =常数
上式表明:当s在在半径为∞的右半圆上运动,映射到 F(s)平面上为一个点,不影响对原点的包围性
-
数出映射曲线绕原点顺时针转了N圈,根据Cauchy辐角原理:N=Z-P
- Z=F(s)RHP-zeros,也是闭环系统RHP-poles
- P=F(s)RHP-poles
-
F(s)=1+G(s)H(s)
- F(s)绕原点旋转⟺G(s)H(s)绕(-1,0)旋转
- F(s)极点=G(s)H(s)极点
⇒闭环系统不稳定极点数目Z=N+P
- N=开环传函G(s)H(s)映射曲线绕(-1,0)顺时针旋转圈数
- P=开环传函G(s)H(s) RHP极点数
闭环稳定⟺N=−P
若开环系统稳定:闭环稳定⟺开环映射曲线不包围(-1,0)
-
修正Nyquist回线
由于Cauchy辐角原理要求不经过零极点,则当G(s)H(s)在虚轴上存在开环零极点时需要以一个无穷小半圆绕过之,并重新绘制G(s)H(s)映射曲线,常常遇到的是位于原点的极点
F(s)=1+βsv∏(s−pi)∏(s−zi),s=ϵeiθ∣θ=0→2π,取极限ϵ→0
G(s)H(s)=βsv∏(s−pi)∏(s−zi)=Ksv∏(τis+1)∏(Tis+1)∣s=limϵ→0ϵeiθ=ϵvKe−jvθ∣limϵ→0=∞e−jvθ
上式表明:平面上原点附近的无限小半圆映射到 F(s)平面上为半径无限大的圆弧,该圆弧的角度从v2π开始按顺时针方向转到 −v2π终止
-
N的快速计数
为了方便计算G(s)H(s)映射曲线绕(-1,0)顺时针旋转圈数,定义N+&N−1
- 正穿越N+:映射曲线向上穿越(-∞,-1)区域次数
- 负穿越N−:映射曲线向下穿越(-∞,-1)区域次数
- N=N+−N−
正穿越:相角减少;负穿越:相角增加
-
实轴对称性
由于零极点共轭,关于实轴对称&奈氏回线关于实轴对称,最终的映射曲线也关于实轴对称。在绘制映射曲线时,只需绘制虚轴 s=0→j∞和s=∞eiθ∣θ=2π→0的部分,剩余关于实轴对称即可
Bode
Relationship with Nyquist
| Nyquist |
Bode |
| 单位圆 |
0dB 幅度线 |
| 负实轴 |
−π 相位线 |
| 正穿越(-∞,-1)区域 |
幅度>0dB时,相频曲线向下穿越−π线 |
| 负穿越(-∞,-1)区域 |
幅度>0dB时,相频曲线向上穿越−π线 |
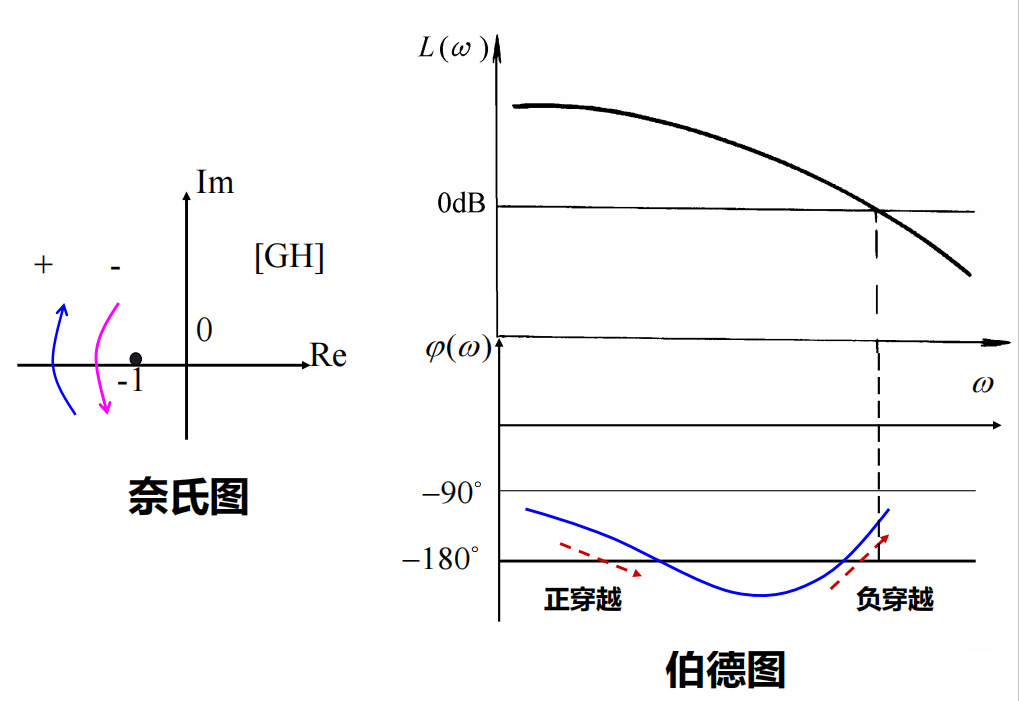
Bode Criteria
注意: 奈氏判据中, w是由 −∞→+∞,伯德图中w是由 0→+∞, 由对称性:对应的映射曲线绕(-1,0)顺时针旋转次数需要➗2修正
- 始于-180°往上是算半次负穿越
- 始于-180°往下是算半次正穿越
- P→2−P
闭环稳定⟺开环 Bode Plot中大于 0dB 区域,相频曲线穿越−π线正负次数之差 N=2−P,P 为 G(s)H(s) 的RHP-poles数目
若开环系统稳定:闭环稳定⟺开环 Bode Plot中大于 0dB 区域,相频曲线穿越−π线次数(正负穿越次数之差)为零
Margin
用来衡量闭环系统的相对稳定性(Relative Stability),分为增益裕度和相角裕度
Margin in Nyquist
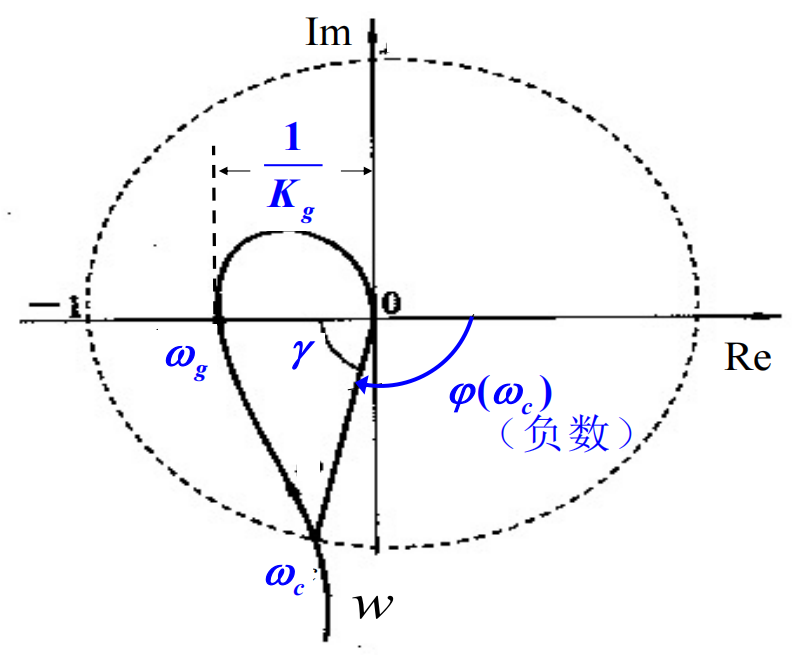
Gain Margin(dB)
表示系统增益可以增大/需要减少多少倍,恰好达到临界稳定
- 相角剪切频率wg:随w增大,开环映射曲线辐角达到−π的频率
- Kg=∣G(s)H(s)∣s=jwg1, GM=−20log(Kg)
Phase Margin(°)
表示系统相角可以滞后/需要超前多少度数,恰好达到临界稳定
-
增益剪切频率:随w增大,开环映射曲线幅值达到1的频率(cut-off)
-
γ=180°+ϕ(wc), 其中ϕ(wc)=∠(G(s)H(s)1)∣s=jwc往往为负数, PM=γ
Margin in Bode
利用Bode和Nyquist的对应关系,从Bode Plot中快速得出GM&PM
直观快速得到 GM&PM
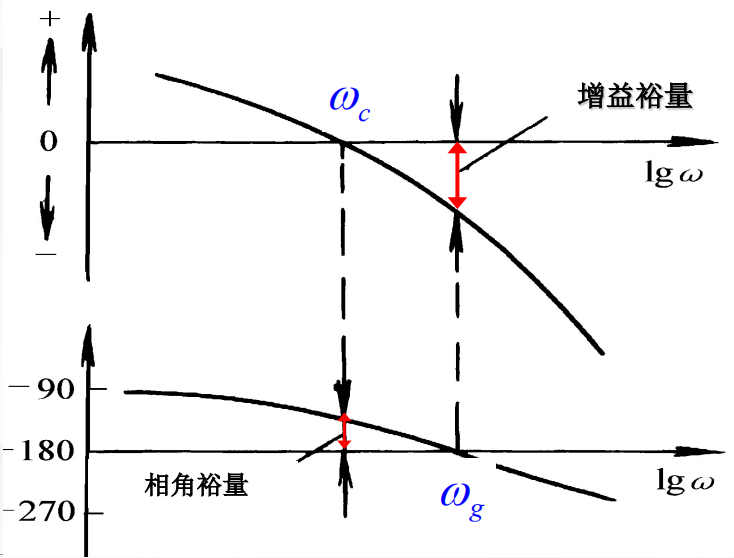
Stability Estimation by Margin
利用PM&GM的正负号判断系统的稳定性
Conclusion
结论:开环稳定时闭环稳定等价于PM>0且GM>0;开环不稳定系统时该准则失效
原因:开环稳定时无RHP开环极点,P=0,闭环稳定等价为Nyquist映射曲线不包围(-1,0),这才能和PM>0&GM>0等价,而开环不稳定时不行(例如SpecialCase3)
Nyquist或Bode Criteria对任何系统始终成立
本质即衡量了奈氏回线的映射曲线距离包围(-1,0)有多近
值得指出:利用PM&GM正负判定稳定性是否成立和是否是最小相位系统无关(和最小相位系统有关的是:应用Bode定理利用零极点的模快速描绘Bode Plot),最小相位系统只是PM&GM二者统一,一个大于零另一个必然大于零,判断一个正负号即可判定系统闭环稳定性;不过最小相位系统因为没有RHP零极点,必然开环稳定,必然可应用该方法,而非最小相位系统仍然可能稳定(只有RHP零点情况),仍可应用该方法
More:开环不稳定可以应用 PM、GM正负号判断吗?
对于开环不稳定的非最小相位系统,稳定的必要不充分条件是:GM<0&PM>0
即至少要包围(-1,0)一次,但是稳定裕度无法具体判断包围了几次
Special Cases
-
幅频多次穿越0dB,wc判定问题 & 相频多次穿越−π线,wg判定问题
- 幅频多次穿越0dB,存在多个不同的穿越频率,对应多个PM值
- 相频多次穿越−π线,存在多个不同的截止频率,对应多个GM值
PM&GM均取最小值,以得到最保守的稳定性估计
本质即映射曲线什么时候离(-1,0)最近
向量裕度:映射曲线到点(-1,0)的最近距离
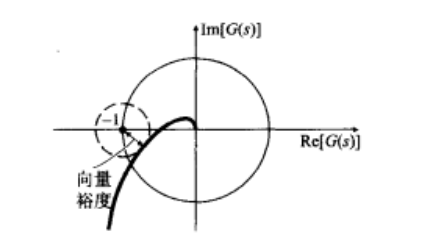
-
相频多次穿越−π线,可能出现条件稳定情况,GM失去意义
这是由于(-1,0)在曲线左侧导致的,此时随着增益加大,其逐步向曲线右侧移动,不同时期曲线的稳定性不同,即较小增益可能不稳定而较大却增益稳定,GM失去其意义
此时具体稳定性要根据Bode Criteria判断,Razavi书上提出对开环稳定系统,相频曲线穿越偶数次稳定,奇数次不稳定就是来源于此
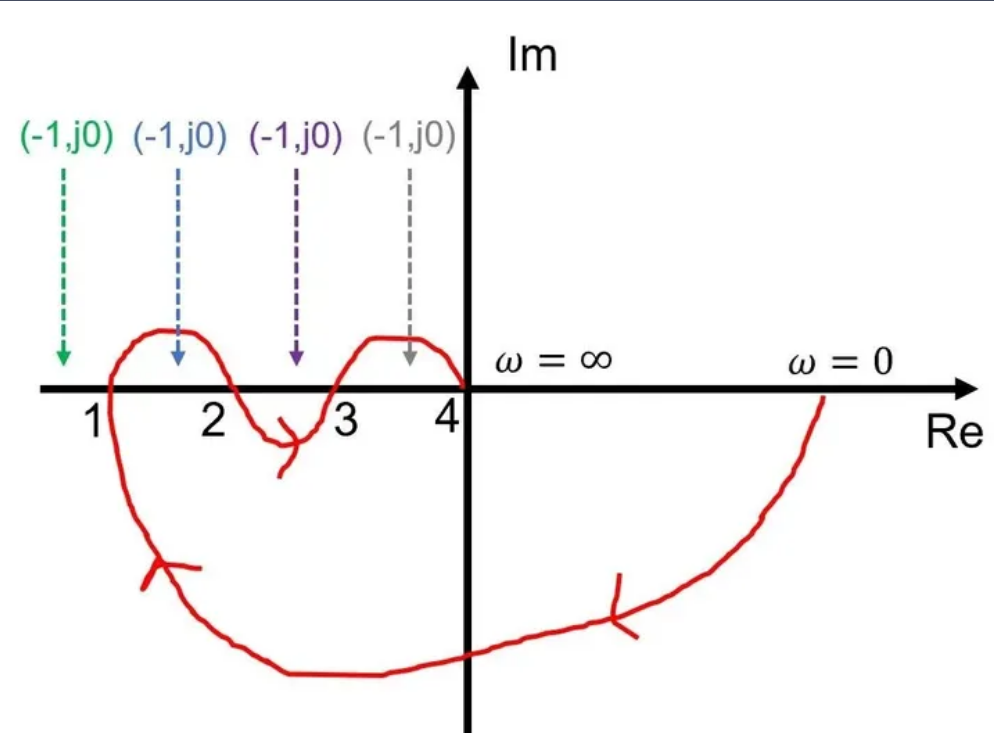
-
开环不稳定的非最小相位系统
开环传递函数L(s)=s(s−1)5(s+3),增益裕量GM<0,相位裕量PM>0,但闭环系统稳定
Barkhausen’s Criteria
闭环系统当某个频率w使得整体phase shift 360°形成正反馈且 magnitude≥1时,系统不稳定,等号处系统等谐震荡。对于负反馈系统:开环传递函数phase shift达到-180°且 magnitude≥1
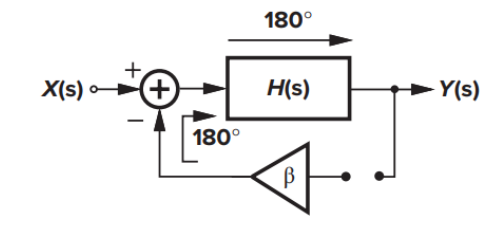
震荡的必要不充分条件(有些系统满足巴克豪森条件但不震荡)
表现在Bode Plot中:某些频率段上的曲线存在Gain>0&phase shift>180°,系统依然稳定(详见Special Circuits)
失效的原因可以从Bode Plot的构成来理解:Bode Plot虽然完全描绘了映射曲线的幅度、相角特性,但是忽略了零极点的相对位置特性,仅仅包含了零极点的模的信息,必然和Nyquist Criteria中的映射曲线平面相比,存在局限性
Special Circuits
-
三阶CPPLL
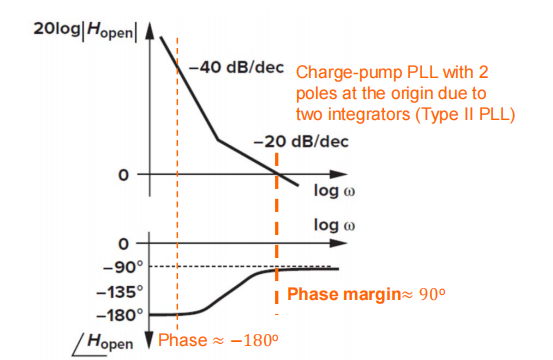
原点处存在两个极点,低频段按Barkhausen’s Criteria不稳定,实际稳定
-
靠近的多个零极点
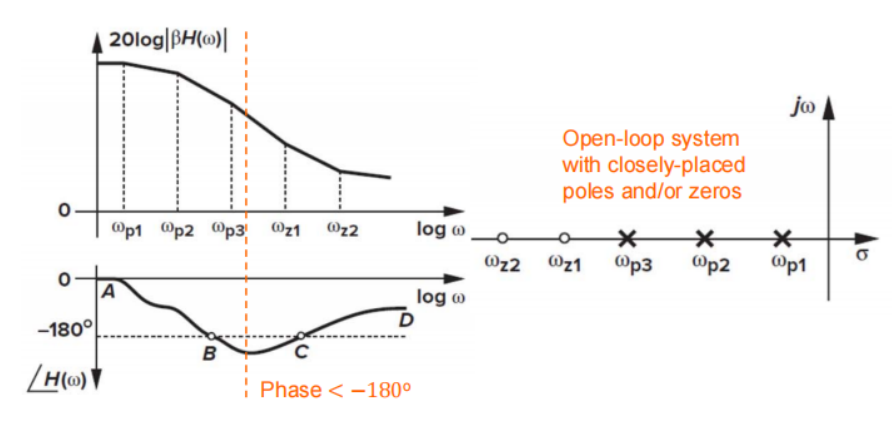
中频段按照Barkhausen’s Criteria不稳定,实际稳定
实际电路设计要求一定要把零极点推远且相互远离,不然很难分析!
值得指出:这两个都是开环稳定系统,仍然能用PM和GM均正的方法判断稳定性(前者因为PM、GM只看wc&wg处,后者为SpecialCase2),只是Barkhausen’s Criteria失效;作为始终通用的Nyquist/Bode Criteria自然也成立