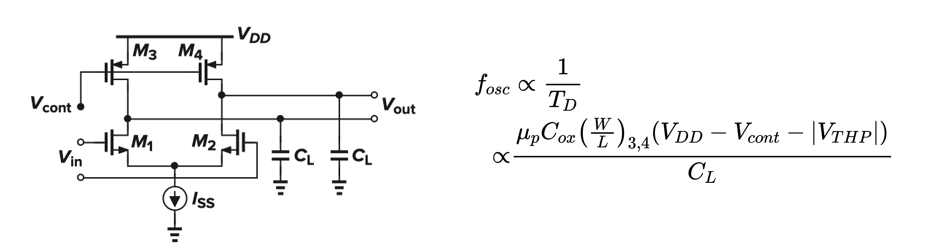Basic Intro
基本概念
比较输出和输入的相位差的反馈系统,利用外部输入的参考信号控制环路内部的震荡信号的频率和相位,使得输出信号与外部参考信号同步
值得指出,PLL中常常考虑相位阶跃的响应
基本组成
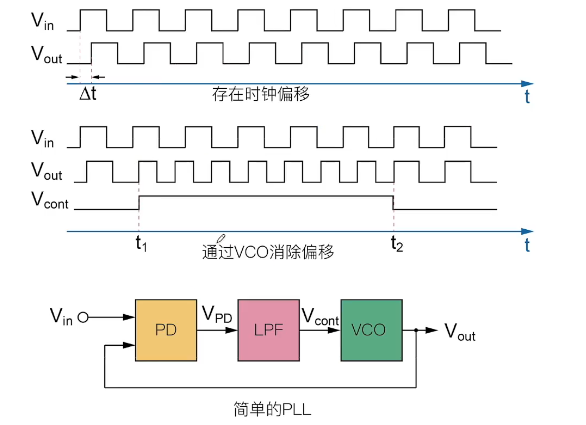
-
Vin:晶振产生的标准时钟信号
-
PD: Phase Detector,鉴相器
比较输入输出相位差,产生监测信号VPD,包含低频成分和高频成分
-
LPF: Low Pass Filter,低通滤波器
低通滤波VPD产生Vcont,低频分量较为稳定
-
VCO: Voltage Controlled Oscillator,压控振荡器
根据Vcont改变Vout频率,最终和输入同步,PLL进入锁定状态
锁定状态相位差为 0,但存在 offset
主要应用
为什么不导线直接连接输入参考信号和输出?(why PLL?)
-
利用分频器:频率合成器
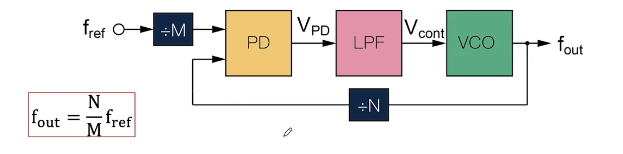
-
时钟恢复和数据重定时
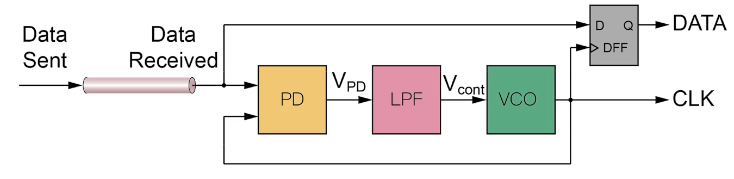
PD鉴相器
理想: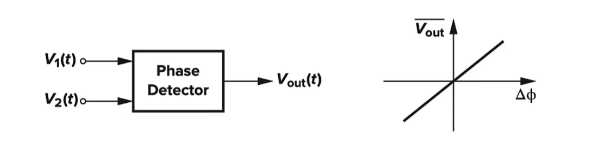
利用异或门简单实现: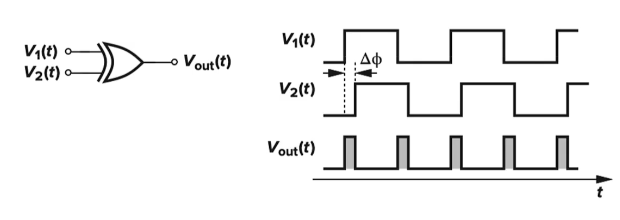
使用异或门近似的PD输出的VPD存在高频分量,VPD才满足需求
串联LPF输出:即实现了取平均
注意:使用异或门,上升和下降沿都会存在脉冲凸起信号
PFD with CP
PFD&CP:鉴相鉴频器&电流泵
应用PFD&CP的PLL叫 CP PLL(电流泵锁相环)
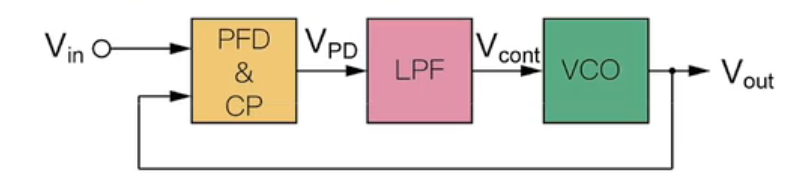
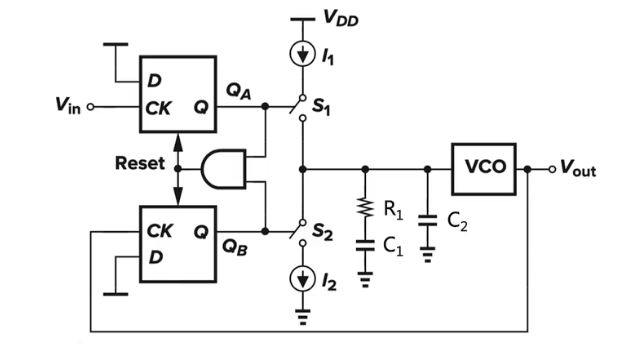
PFD鉴相鉴频器
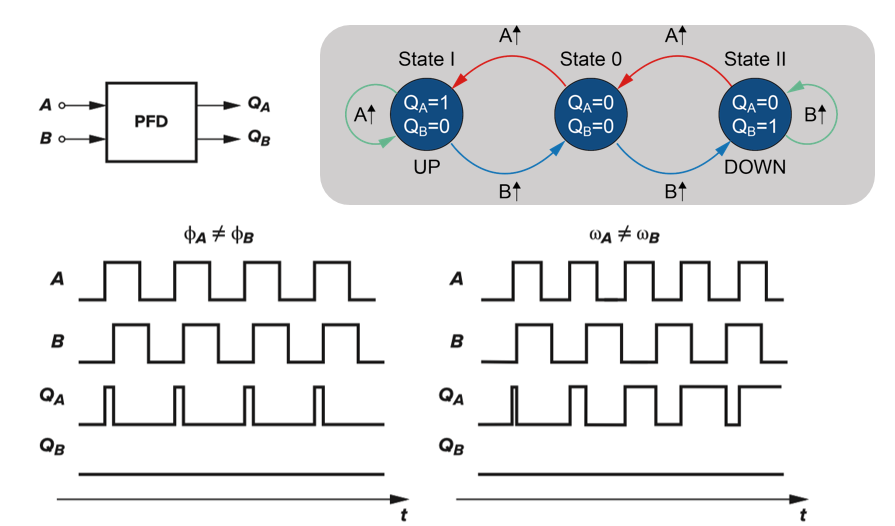
双端输出,UP/DOWN状态:加大/降低频率
能鉴别相位和频率,加速 PLL的锁定
PLL开始工作时,参考信号可能与输入信号偏差很大,但因为PD仅能检查相位偏差,其频率捕获范围较小,导致PLL需要逐步进入锁定状态 ,响应时间较长。
改进:使用鉴频鉴相器(Phase/Frequency Detector,PFD)
反馈的频率与输入频率不相等时,则鉴频鉴相器首先进行鉴频,通过比较反馈信号与输入的频差产生电压作用在电荷泵上,使LPF的输出电压改变。通过电压的作用使输出频率向输入频率逐渐逼近,直到两者频率相等,此时启动鉴相功能,逼近输入频率与输出频率的相位
具体可以采用两个异步清零的D触发器和一个与门实现:
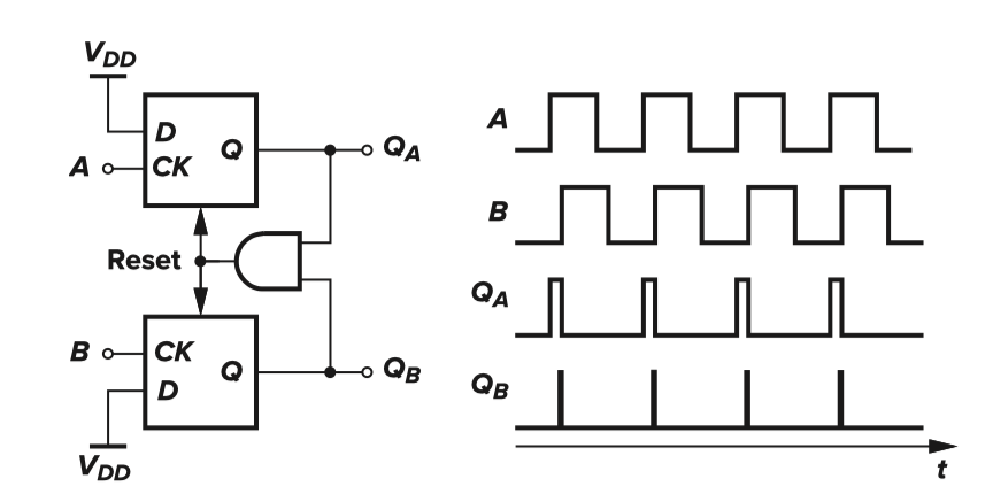
- A升高→QA高电平
- B升高→QB高电平
- QA&QB高电平→ Reset QA&QB
由于D触发器和与门内部存在延时,实际上可能会产生信号毛刺,带来不稳定性:选择在与门到RESET端再加一个delay(可以用多个反相器实现),进而消除竞争
这会让QA&QB都多出delay的高电平:没有关系,因为本来就要差分输出
CP电荷泵
PLL中关心的是QA&QB两者平均输出,所以需要将这两个输出经过低通滤波后,再作差分输出。但是更普遍的做法是在PFD和环路滤波器之间再插入一个电荷泵(Charge Pump, CP)电路来先进行双端转单端实现差分。
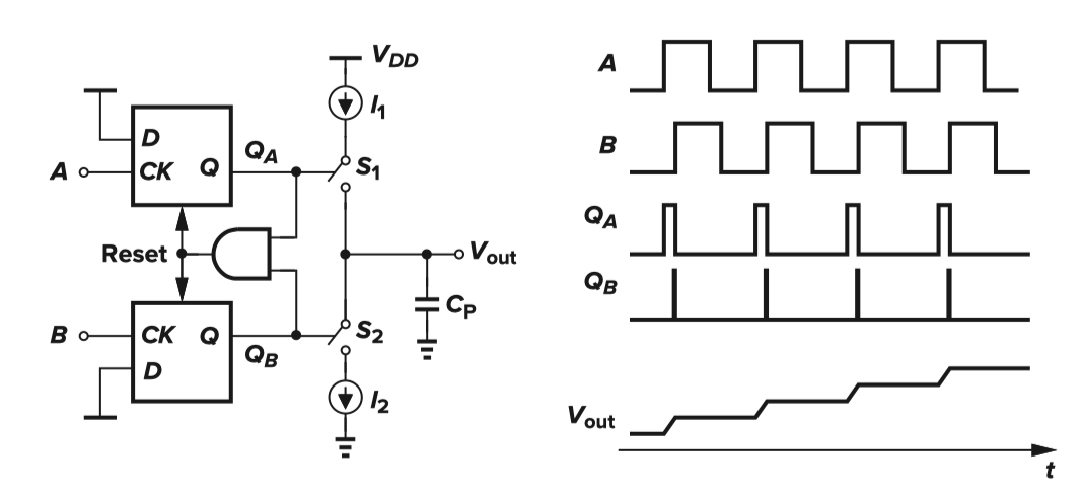
- I1和I2被称为上拉电流和下拉电流,它们的额定值一般是相等的
- QA=QB,开关S1和S2均断开,Vout保持不变
- QA高,QB低,I1对CP充电,Vout升高
- QA低,QB高,I2对CP充电,Vout降低
线性模型近似
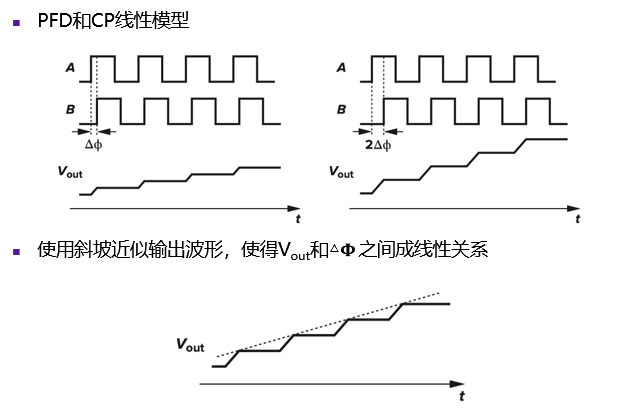
每个周期T,输出电压增加CPIPϕ2πT→最终输出电压Vout=∫otCP2πIPϕdt(单位时间增加电压对总时间的积分 )
Iout=tQout=tVoutCP=2πIPt∫0tϕdt=2πIPϕ
⇒TPFD&CP(s)=ϕIout=2πIP,记作KPD
LPF低通滤波器
工作原理
实际上起到了一个求平均值的作用,把PD输出的高频信号消除,输出稳定的直流信号作为VCO的输入
具有滞后的特性:LPF牺牲了响应灵敏度,换取了响应稳定度
以PLL对相位阶跃响应为例:
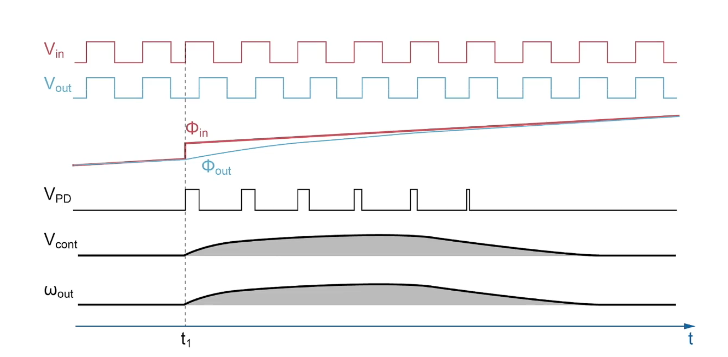
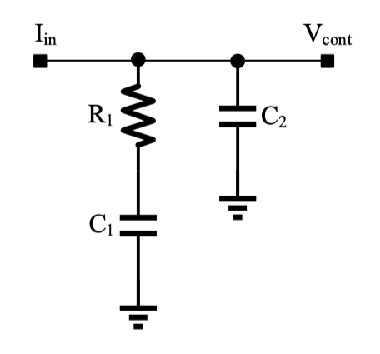
实际的 LPF常常采用二阶 RC电路来提升系统稳定性、减小输出电压的纹波
C2大约为 C1的 81∼101
线性模型近似
HLPF(s)=IinVcont=R1C1C2s2+s(C1+C2)1+sR1C1
VCO压控振荡器
其没有输入信号,但是可以持续产生一个周期性的电压信号输出,通常用于产生时钟信号,PLL中用于改变输出信号的相位
起振条件(巴克豪森准则)
震荡的必要条件,但不是充分的
目前还没有一个既是充分条件也是必要条件的简单振荡准则
- 环路相移 n⋅2π→∠H(jw0)=π (n=1)
- 环路增益不小于1→∣H(jw0)∣≥1 (0 dB)
探讨:常见结构能否发生震荡?
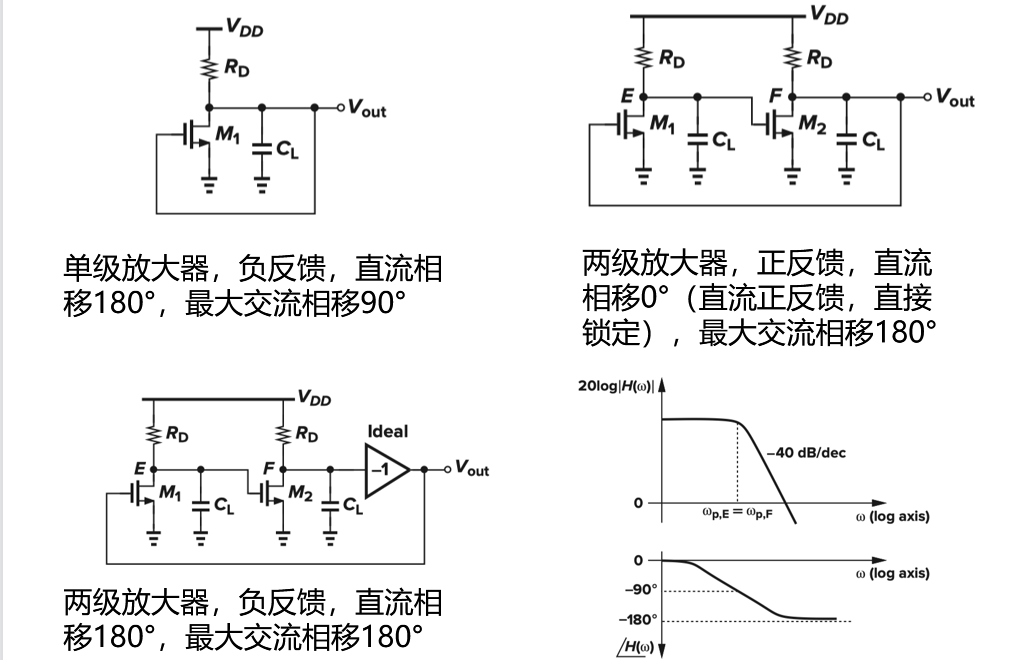
单级增益为负,负反馈带来环路phase shift 180°;一个极点至多90° phase shift
⇒理论上两级放大器相位条件满足震荡,但此时频率在第二极点十倍带宽外,幅值往往很小,低于单位增益,难以满足震荡的增益条件
环形振荡器
环形震荡器一定要奇数级吗?(单端的Yes,why???)
No!可以用全差分的偶数级
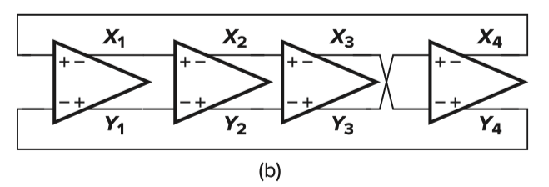
增幅的震荡最终会饱和,而不会无穷增加:即实际震荡电路会和线性模型有偏差(随着振幅增加,系统非线性程度增加)
实际震荡频率为 f=2Tdelay,all1=2NTdelay,cell1
线性模型近似
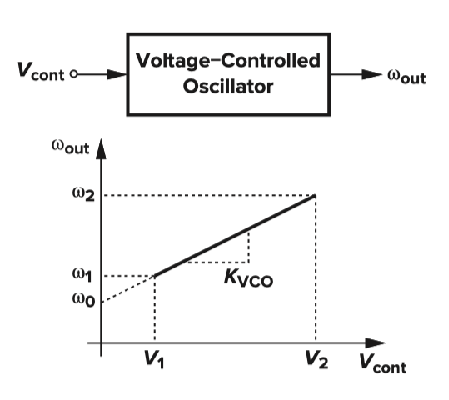
ϕout=ϕ0+∫wdt, w=w0+KVCOVcont→ϕout=ϕ0+wot+KVCO∫Vcontdt
关心盈出相位ϕext=KVCO∫Vcontdt
TVCO(s)=Vcontϕext=sKVCO
电路实现
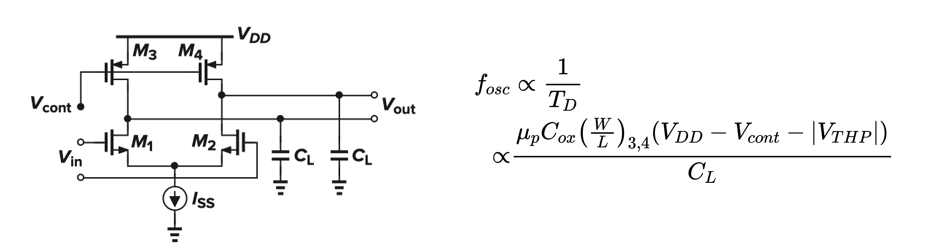
Tdelay本质就是RC充放电延迟,Ron和Vcont相关
简单的Delay Cell会导致输出共模电平和Vcont相关,可改进偏置结构解决
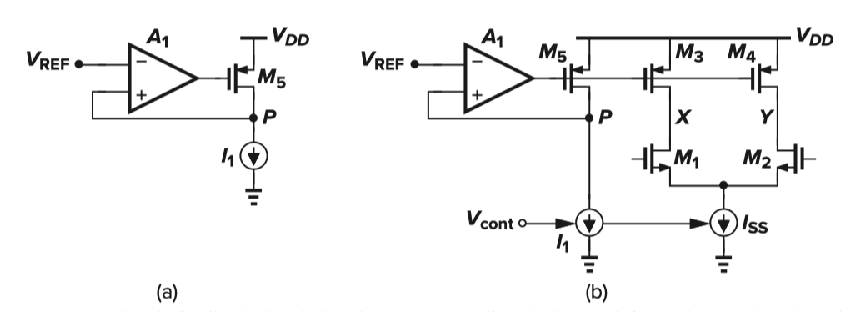
钳位PXY点电压和Vref一致(共模输出电平IR drop相关,I和R都和Vcont相关抵消)
Vcont同时控制Iss大小实现Voltage control: fosc∝Ron3,4CL1∝(VDD−Vref)CLIss
三阶CPPLL稳定性设计
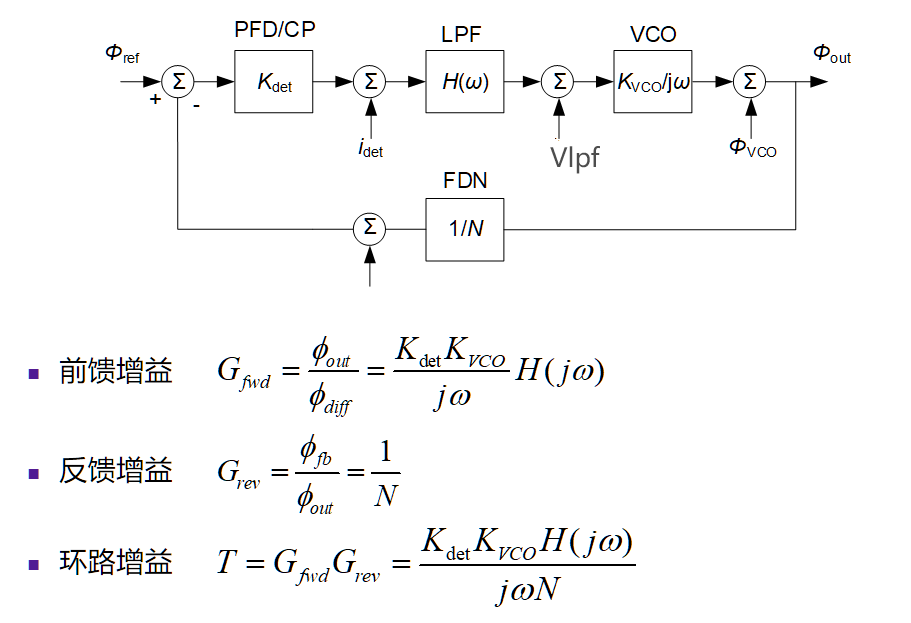
总结PLL的结构和线性模型: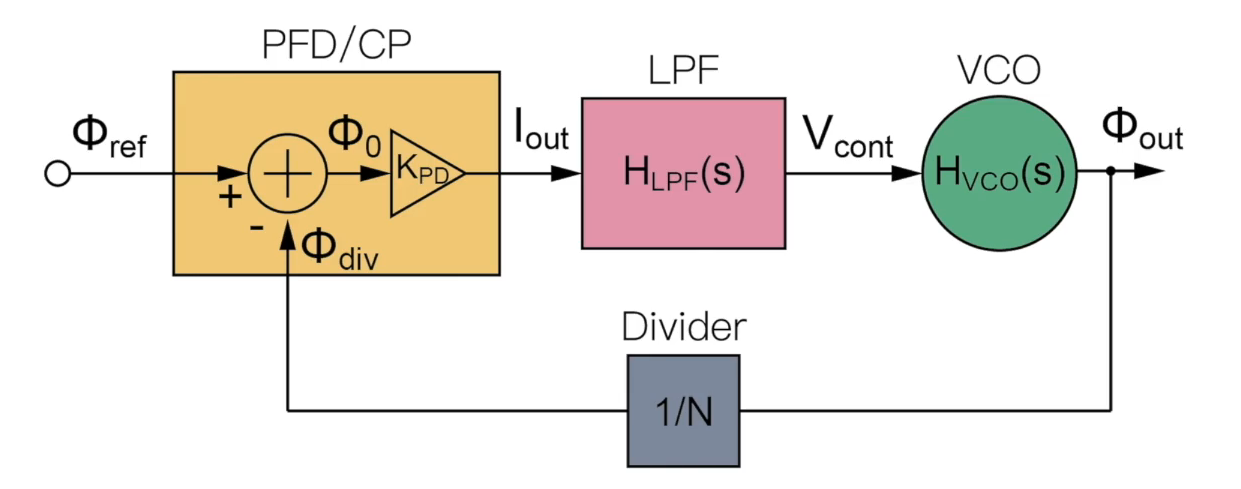
- PFD&CP:将相位信号转化到电流信号
- LPF:将电流信号转化到电压信号
- VCO:将电压信号转化到相位信号
- Divider:分频器,形成相位信号反馈
Loop gain G(s)=N12πIpR1C1C2s2+s(C1+C2)1+sR1C1sKVCO
Close loop T(s)=ϕrefϕout=1+G(s)NG(s)
Bode plot针对open loop gain G(s):存在两个原点处极点p1,2=0,一个LHP极点p3=−R1C1C2C1+C2和一个LHP零点z1=−R1C11
在设计PLL时候往往为了稳定性,使得unit gain frequency处PM最大
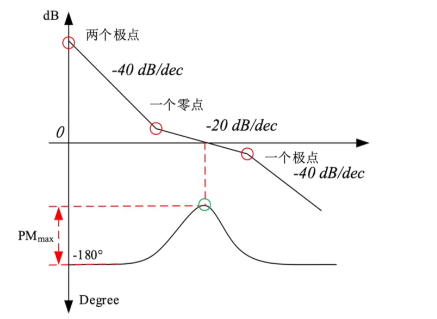
值得指出:零点处有两个极点直接带来-180°phase shift,但不意味不稳定
PM=π−2π∗2+arctan(z1w)−arctan(p3w)=arctan(z1w)−arctan(p3w)
PM对w求导,得到极值点在w=p3z1处取到,希望此处G(s)=1
设计时:对于给定的PMmax和带宽wu,求解LPF的R1,R2,C1
arctan(z1wu)−arctan(p3wu)=PMmax
p3z1=wu, p3=−R1C1C2C1+C2, z1=−R1C11
G(s)∣s=wu=1
求解上述方程即可,具体使用MATLAB脚本:
1
2
3
4
5
6
7
8
9
10
11
12
13
| clear
wu=2*pi*0.8e6;
pm=60/180*pi;
N=10;
Icp=44e-6;
Ios=0;
Kpd=Icp/2/pi;
Kvco=250e6*2*pi;
wp=wu*cos(pm)/(1-sin(pm));
wz=wu^2/wp;
C2=1/N*Kpd*Kvco/wu^2*sqrt(wz/wp)
C1=(wp/wz-1)*C2
R1=1/C1/wz
|
Phase Noise相位噪声
Basic Concepts
频率偏移Δf下的1HZ带宽内噪声能量与中心频率f0下的1HZ带宽内噪声能量的比值
dBc form: SΦ(Δf)=10log(Pf0PΔf)
在时域上使用时间抖动(Jitter)衡量相位噪声
-
周期抖动(Cycle-Jitter)
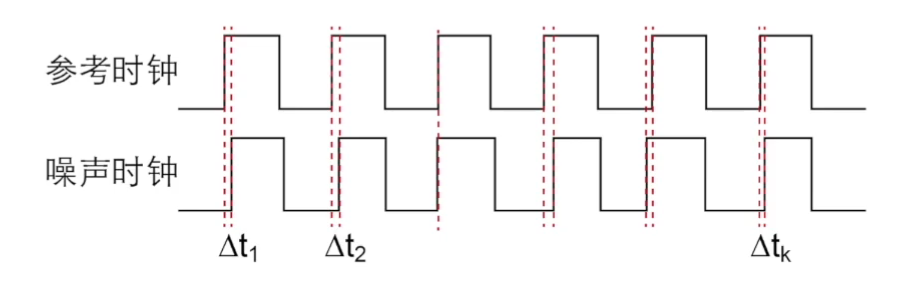
计算{Δtk}的均方根
-
周期周期抖动(Cycle-Cycle Jitter)

计算自身周期间ΔT2−ΔT1,无需参考时钟
Jitter和SΦ(Δf)存在数学对应关系:
A=∫0∞SΦ(f)df,一般实际计算1HZ到几十MHZ的积分即可
Jitter=2πf02⋅10A/10
这是哪一个Jitter????
相位噪声仿真计算
-
Transient仿真后,构建眼图,计算系统Jitter
系统自带的误差,类似offset,未考虑器件噪声
-
Transient Noise 仿真后,构建构建眼图,计算系统+噪声Jitter
考虑器件噪声,仿真计算综合Jitter,但不好分析某一部分的影响
-
Pnoise模块仿真+传递函数
分析各个模块对输出Jitter的影响,good!
具体分析步骤:

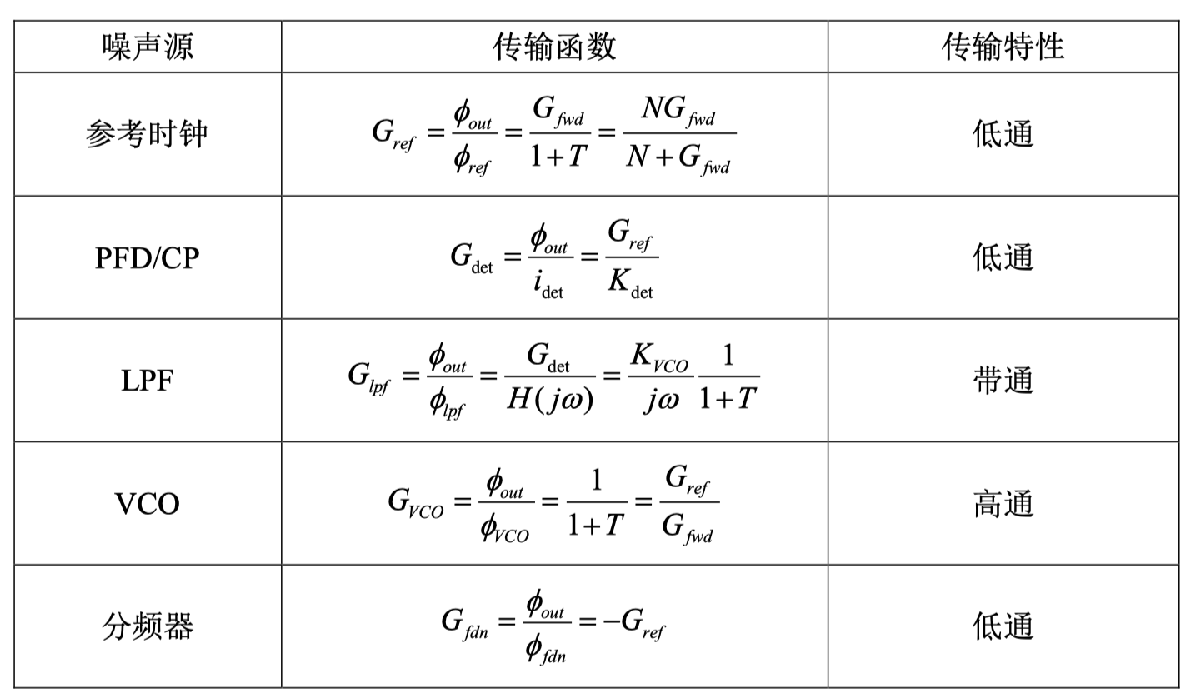

具体仿真举例: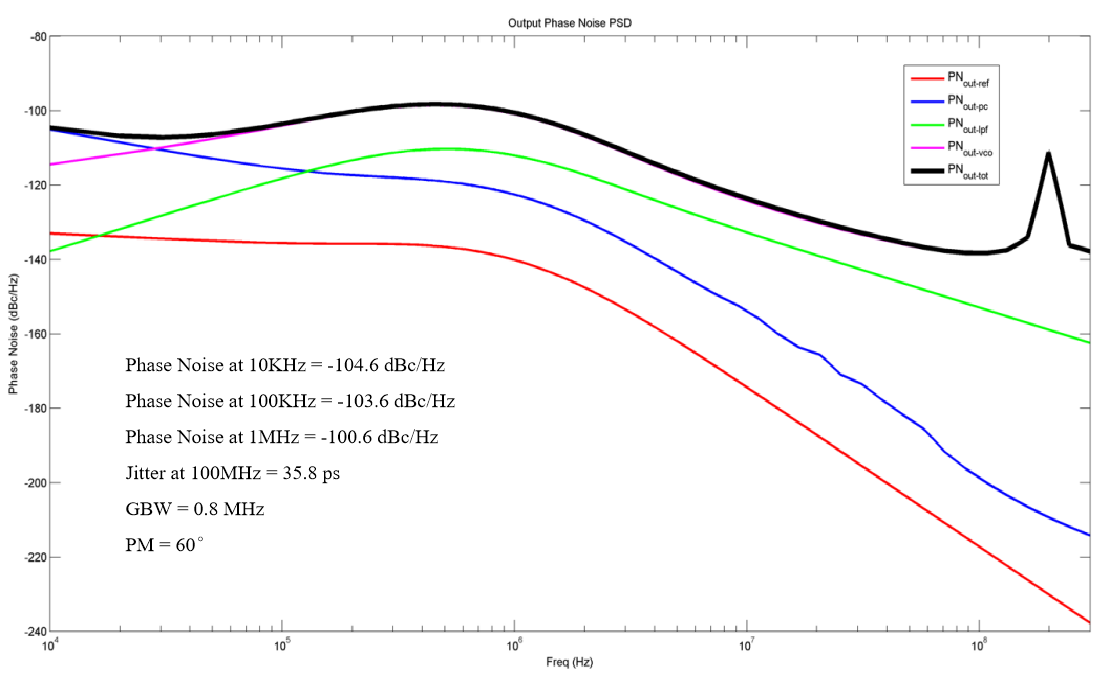
可以看到,OUTPUT处的主要的相位噪声来自于VCO模块
DLL
Delay Locked Loop延时锁定环:一种PLL的变形,实现对特定延时时间的锁定(即产生特定的精确延时delay)
由鉴相鉴频器、电荷泵、LPF、压控延时线(VCDL)组成
基本工作原理
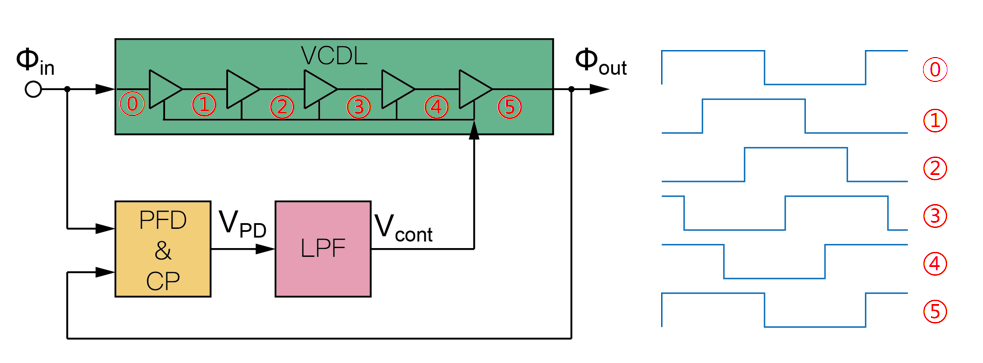
-
ΦinΦinΦin经过VCDL产生N个DelayCell后的Φout
-
Φout&Φin经过PFD&CP、LPF后产生Vcont作为VCDL的电压控制,形成负反馈:Φout相位滞后Φin,Vcont使得VCDL延时减少,进而Φout相位逼近Φin,反之亦然
-
最终Φout和ΦinΦin相位一致:Ntdelay,cell与Tclk精确相等
此时取出Vcont+一个DeLay Cell可以形成精确的NTclk的延时单元
小信号模型
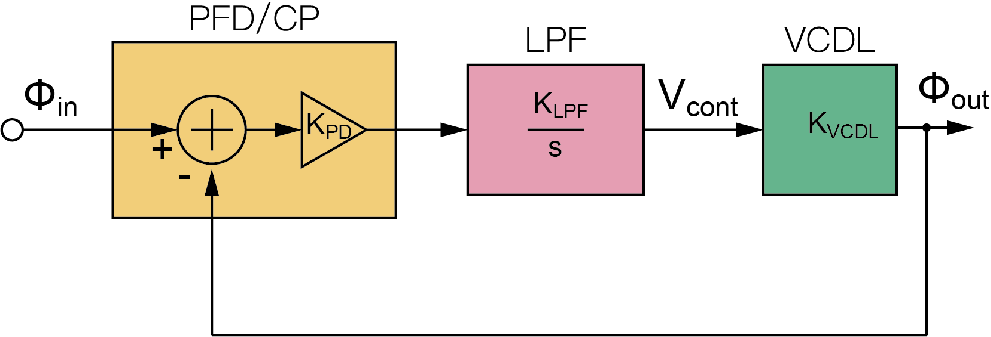
G(s)=KPD⋅sKLPF⋅KVCDL:一阶系统,无条件稳定!
与CPPLL不同,LPF只用一个电容实现,且VCO替换成了VCDL
无Jitter积累???
Delay Cell&VCDL Implement
Current-starved 反相器实现Delay Cell的拓扑及VCDL实现
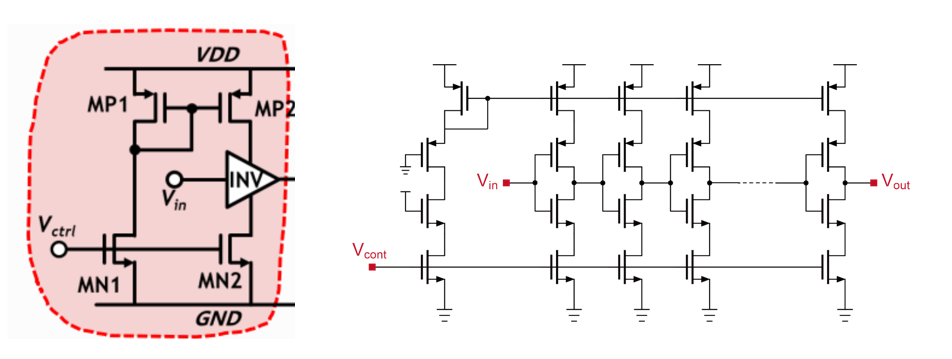
偏置电路新增gate连接VDD&GND的NMOS&PMOS:使bias的管子拓扑与右侧delay cell一致,工作状态更接近
当Vctrl增大,电流镜电流增大,使得每个cell delay的时间下降,形成一一对应关系
数集知识???